如图,矩形ABCD中,AB=6,BC=2 ,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t,使△AOH是等腰三角形?若存大,求出对应的t的值;若不存在,请说明理由.
某企业为重庆计算机产业基地提供电脑配件,受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
| 月份x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 价格y1(元/件) |
560 |
580 |
600 |
620 |
640 |
660 |
680 |
700 |
720 |
随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;
(2)若去年该配件每件的售价为1000元,生产每件配件的人力成本为50元,其它成本30元,该配件在1至9月的销售量p1(万件)与月份x满足函数关系式p1=0.1x+1.1(1≤x≤9,且x取整数)10至12月的销售量p2(万件)与月份x满足函数关系式p2=﹣0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(3)今年1至5月,每件配件的原材料价格均比去年12月上涨60元,人力成本比去年增加20%,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时每月销售量均在去年12月的基础上减少0.1a%.这样,在保证每月上万件配件销量的前提下,完成了1至5月的总利润1700万元的任务,请你参考以下数据,估算出a的整数值.
(参考数据:992=9901,982=9604,972=9409,962=9216,952=9025)
如图,梯形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD.过点C作CE⊥AB于E,交对角线BD于F,点G为BC中点,连接EG、AF.
(1)求EG的长;
(2)求证:CF=AB+AF.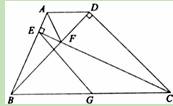
为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:
(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
如图,在平面直角坐标系x0y中,一次函数y=kx+b(k≠0)的图象与反比例函数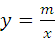 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE= .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.