某市有A,B,C,D四个大型超市,分别位于一条东西走向的平安大路两侧,如图所示,请建立适当的直角坐标系,并写出四个超市相应的坐标.
如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标__________;
(2)顺次连接(1)中的所有点,得到的图形是__________图形(填“中心对称”、“旋转对称”、“轴对称”);
(3)指出(1)中关于点P成中心对称的点__________.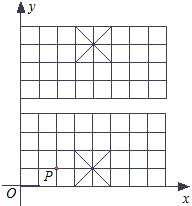
图1、图2是北京市2006﹣﹣2010年户籍人口数和户籍65岁及以上人口数的统计图和2010年北京市户籍人口各年龄段统计图
请你根据以上信息解答下列问题:
(1)2010年北京市65岁及以上人口数约有多少万人?(结果保留四位有效数字)
(2)补全条形统计图;
(3)根据联合国教科文组织的规定,一个国家(地区)65岁以上的人口占人口总数的7%以上,这个国家(地区)则进入了老龄化社会.由此可见北京市已经步入了老龄化社会.小明通过学习知道养老方式有三种:家庭养老、机构养老和社区养老.小明同学调查了他所居住小区的120名65岁及以上的老人,选择养老方式如下表所示.如果按照小明的统计数据,请你通过计算估计,2010年北京市65岁及以上的老人选择机构养老的约有多少万人?
小明居住小区65岁及以上的老人选择养老方式的人数统计表.
| 养老方式 |
家庭养老 |
机构养老 |
社区养老 |
| 人数(人) |
72 |
18 |
30 |
中小学生作业负担过重现象已经引起社会各界关注,各中小学校积极采取措施,“减负增效”势在必行.某中学在新学期开始就实行多种措施,力求“减负增效”,并取得理想效果.该校对在校300名学生就实施措施后的每日作业用时减水率进行随机调查,调查统计的数据制成如下统计图表:
| 每日作业用时减水率x |
x<30% |
30%≤x<40% |
40%≤x<50% |
x≥50% |
| 学 生 数 |
60 |
120 |
78 |
42 |
(1)被调查300名学生的每日作业用时减水率的中位数在什么范围内?
(2)扇形统计图中“30%≤x<40%”对应扇形的圆心角为_______度;
(3)该校在校学生有2400人,在实施“减负增效”后,每日作业用时减水率不低于40%的学生约有多少人?
某校初二年级全体320名学生在参加电脑培训前后各进行了一次水平相同的考试,考试都以同一标准划分成“不合格、合格、优秀”三个等级,为了了解培训的效果,用抽签的方式得到其中32名学生的两次考试等级,所绘的统计图如图所示,结合图示信息回答下列问题:
(1)这32名学生培训前考分的中位数所在的等级是_______;
(2)这32名学生经过培训后,考分等级“不合格”的百分比是_______;
(3)估计该校整个初二年级中,培训后考分等级为“合格”与“优秀”的学生共有_______名;
(4)你认为上述估计合理吗?理由是什么?