图1、图2是北京市2006﹣﹣2010年户籍人口数和户籍65岁及以上人口数的统计图和2010年北京市户籍人口各年龄段统计图
请你根据以上信息解答下列问题：
（1）2010年北京市65岁及以上人口数约有多少万人？（结果保留四位有效数字）
（2）补全条形统计图；
（3）根据联合国教科文组织的规定，一个国家（地区）65岁以上的人口占人口总数的7%以上，这个国家（地区）则进入了老龄化社会．由此可见北京市已经步入了老龄化社会．小明通过学习知道养老方式有三种：家庭养老、机构养老和社区养老．小明同学调查了他所居住小区的120名65岁及以上的老人，选择养老方式如下表所示．如果按照小明的统计数据，请你通过计算估计，2010年北京市65岁及以上的老人选择机构养老的约有多少万人？
小明居住小区65岁及以上的老人选择养老方式的人数统计表．
| 养老方式 |
家庭养老 |
机构养老 |
社区养老 |
| 人数（人） |
72 |
18 |
30 |
某中学就到校的方式问题对初三年级的所有学生进行一了次调查，并将调查结果制作了表格和扇形统计图，请你根据图表信息下列各题：
(1)补全下表：
| 初三学生 人数 |
步行 人数 |
骑车 人数 |
乘公交车 人数 |
其它方式 人数 |
| 60 |
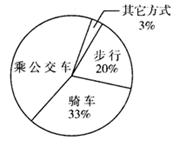
(2)在扇形统计图中，“步行”对应的圆心角的度数为.
先化简，再求值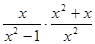
，其中
．
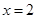如图，在平面直角坐标系中，点C的坐标为（0，4），动点A以每秒1个单位长的速度，从点O出发沿
轴的正方向运动，M是线段AC的中点．将线段AM以点A为中心，沿顺时针方向旋转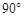
，得到线段AB．过点B作轴的垂线，垂足为E，过点C作
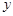轴的垂线，交直线BE于点D．运动时间为
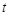秒．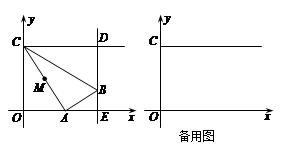
（1）当点B与点D重合时，求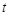的值；
（2）设△BCD的面积为S，当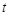为何值时，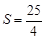
?
（3）连接MB，当MB∥OA时，如果抛物线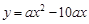
的顶点在△ABM内部（不包括边），求a的取值范围．
如图1，矩形MNPQ中，点E，F，G，H分别在NP，PQ，QM，MN上，若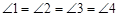
，则称四边形EFGH为矩形MNPQ的反射四边形．图2，图3，图4中，四边形ABCD为矩形，且
，
．
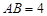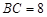理解与作图：
（1）在图2，图3中，点E，F分别在BC，CD边上，试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH．
计算与猜想：
（2）求图2，图3中反射四边形EFGH的周长，并猜想矩形ABCD的反射四边形的周长是否为定值？
启发与证明：
（3）如图4，为了证明上述猜想，小华同学尝试延长GF交BC的延长线于M，试利用小华同学给我们的启发证明（2）中的猜想．
某景区的旅游线路如图1所示，其中A为入口，B，C，D为风景点，E为三岔路的交汇点，图1中所给数据为相应两点间的路程（单位：km）．甲游客以一定的速度沿线路“A→D→C→E→A”步行游览，在每个景点逗留的时间相同，当他回到A处时，共用去3h．甲步行的路程s（km）与游览时间t（h）之间的部分函数图象如图2所示．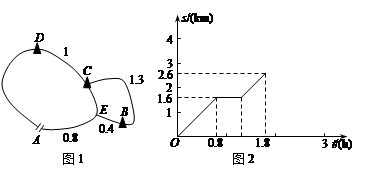
（1）求甲在每个景点逗留的时间，并补全图象；
（2）求C，E两点间的路程；
（3）乙游客与甲同时从A处出发，打算游完三个景点后回到A处，两人相约先到者在A处等候， 等候时间不超过10分钟．如果乙的步行速度为3km/h，在每个景点逗留的时间与甲相同，他们的约定能否实现？请说明理由．