如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标__________;
(2)顺次连接(1)中的所有点,得到的图形是__________图形(填“中心对称”、“旋转对称”、“轴对称”);
(3)指出(1)中关于点P成中心对称的点__________.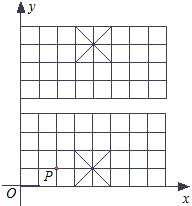
(本题9分)已知关于x的一元二次方程 +6x=4m﹣3有实数根.
+6x=4m﹣3有实数根.
(1)求m的取值范围;
(2)设方程的两实根分别为 与
与
 ,且
,且 =
= ·
· +7,求m的值.
+7,求m的值.
(本题9分)如图,在菱形ABCD中,AB=2 ,∠BAD =60º,AC交BD于点O,以点D为圆心的⊙D与边AB相切于点E.
,∠BAD =60º,AC交BD于点O,以点D为圆心的⊙D与边AB相切于点E.
(1)求AC的长;(2)求证:⊙D与边BC也相切
(本题7分)为了决定谁将获得仅有的一张科普报告入场券,甲和乙设计了如下的一个游戏:口袋中有编号分别为1、2、3的红球三个和编号为4的白球一个,四个球除了颜色或编号不同外,没有任何别的区别,摸球之前将小球搅匀.先甲摸两次,每次摸出一个球;把甲摸出的两个球放回口袋后,乙再摸,乙只摸一个球.如果甲摸出的两个球都是红色,甲得1分,否则,甲得0分;如果乙摸出的球是白色,乙得1分,否则,乙得0分 ;得分高的获得入场券,如果得分相同,游戏重来.
(1)运用列表或画树状图求甲得1分的概率;
(2)这个游戏是否公平?请说明理由.
(本题8分)如图,一次函数 y="kx+b" 的图象与反比例函数y= 的图象交于 A(﹣2,1),B(1,n)两点.
的图象交于 A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)连OB,在x轴上取点C,使BC=BO,并求△OBC的面积.
(本题8分)如图,在由边长为1的小正方形组成的网格中,△ABC的顶点均落在格点上
(1)在图中画出△ABC关于点O成中心对称的图形△A′B′C′;
(2)在(1)的作图过程中,点A,B,C分别绕点O旋转_________°,求点C在旋转过程中所走过的路径长.