如图,在△ABC中,∠ABC=90°,∠A=30。,斜边AC上的中线BD=2,现沿BD将△BCD折起成三棱锥C-ABD,已知G是线段BD的中点,E,F分别是CG,AG的中点.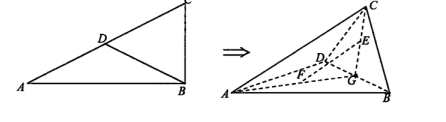
(1)求证:EF//平面ABC;
(2)三棱锥C—ABD中,若棱AC=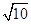 ,求三棱锥A一BCD的体积.
,求三棱锥A一BCD的体积.
如图1,在直角梯形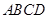 中,
中,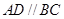 ,
,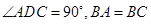 .把
.把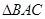 沿
沿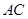 折起到
折起到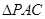 的位置,使得
的位置,使得 点在平面
点在平面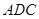 上的正投影
上的正投影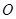 恰好落在线段
恰好落在线段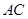 上,如图2所示,点
上,如图2所示,点 分别为棱
分别为棱 的中点.
的中点.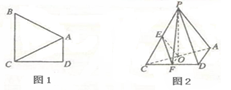
(1)求证:平面 平面
平面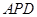 ;
;
(2)求证: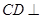 平面
平面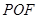 ;
;
(3)若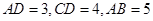 ,求四棱锥
,求四棱锥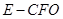 的体积.
的体积.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,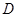 是AC的中点,已知
是AC的中点,已知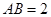 ,
, .
.
(1)求证:OD//平面VBC;
(2)求证:AC⊥平面VOD;
(3)求棱锥 的体积.
的体积.
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且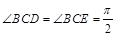 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.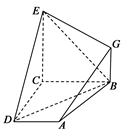
(1)求证: EC⊥CD ;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积.
如图,已知四棱锥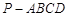 ,底面
,底面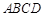 是等腰梯形,
是等腰梯形,
且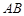 ∥
∥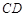 ,
,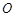 是
是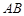 中点,
中点,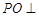 平面
平面 ,
,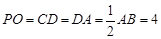 ,
, 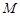 是
是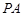 中点.
中点.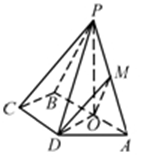
(1)证明:平面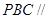 平面
平面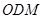 ;
;
(2)求平面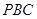 与平面
与平面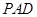 所成锐二面角的余弦值.
所成锐二面角的余弦值.