如图:已知正方形ABCD的边长为2,且AE⊥平面CDE,AD与平面CDE所成角为 .
.
(1)求证:AB∥平面CDE;
(2)求三棱锥D-ACE的体积.
(本小题满分12分)
2008年为山东素质教育年,为响应素质教育的实施,某中学号召学生在放假期间至少参加一次社会实践活动(以下简称活动).现统计了该校100名学生参加活动的情况,他们参加活动的次数统计如图所示.
(1)求这些学生参加活动的人均次数;
(2)从这些学生中任选两名学生,求他们参加活动次数恰好相等的概率;
(3)从这些学生中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
(本题12分)
已知A、B、C的坐标分别为A , B
, B , C
, C ,
,  .
.
(1) 若
 , 求角
, 求角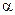 的值; (2) 若
的值; (2) 若 , 求
, 求 的值.
的值.
设函数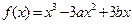 的图像与直线
的图像与直线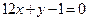 相切于点
相切于点 .
.
(Ⅰ)求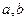 的值;(Ⅱ)讨论函数
的值;(Ⅱ)讨论函数 的单调性。
的单调性。
18.(本小题满分12分)已知函数
(1)求 的定义域;(2)已知
的定义域;(2)已知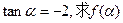 的值.
的值.
(本小题满分12分)在数列 中,前n项和为
中,前n项和为

(1)求数列 是等差数列.
是等差数列.
(2)求数列{ }的前n项和Tn.
}的前n项和Tn.