已知数列
的前
项和
.
(1)求数列
的通项公式;
(2)设
,求数列
的前
项和.
在平面直角坐标系
中,点
到点
的距离比它到
轴的距离多1,记点
的轨迹为
.
(1)求轨迹为
的方程
(2)设斜率为
的直线
过定点
,求直线
与轨迹
恰好有一个公共点,两个公共点,三个公共点时
的相应取值范围.
为圆周率,
为自然对数的底数.
(1)求函数
的单调区间;
(2)求
这6个数中的最大数与最小数;
(3)将
这6个数按从小到大的顺序排列,并证明你的结论.
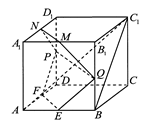
如图,在正方体
中,
,
,
,
,
,
分别是棱
,
,
,
,
,
的中点.求证:
(1)直线
∥平面
;
(2)直线
⊥平面
.
某实验室一天的温度(单位:
)随时间
(单位:
)的变化近似满足函数关系;
.
(1)求实验室这一天上午8时的温度;
(2)求实验室这一天的最大温差.