已知：如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F；当直线EF停止运动时，点P也停止运动．连接PF，设运动时间为t（s）（0＜t＜8）．解答下列问题：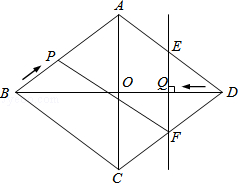
（1）当t为何值时，四边形APFD是平行四边形？
（2）设四边形APFE的面积为y（cm2），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使S四边形APFE：S菱形ABCD=17：40？若存在，求出t的值，并求出此时P，E两点间的距离；若不存在，请说明理由．
从2015年1月7日起，中国中东部大部分地区持续出现雾霾天气。某市记者为了了解“雾霾天气的主要成因”，随机调查了该市部分市民，并对调查结果进行整理，绘制了如下尚不完整的统计图表．
请根据图表中提供的信息解答下列问题：
（1） 填空：m= ，n=，扇形统计图中E组所占的百分比为%．
（2） 若该市人口约有100万人，请你计算其中持D组“观点”的市民人数．
（3） 若在这次接受调查的市民中，随机抽查一人，则此人持C组“观点”的概率是多少？
如图，在平行四边形ABCD中，E，F分别为边AB，CD的中点，BD是对角线，过A点作AG∥DB交CB的延长线于点G ．
（1）求证：四边形DEBF是平行四边形；
（2）如果 ∠G=90°， ∠C=60°， BC=2， 求四边形DEBF的面积．
列方程或方程组解应用题：
某工程队改造一条长2 500米的道路．在改造了1 000米后，为了减少施工对交通造成的影响，采用了新的施工工艺，使每天的工作效率是原来的1．5倍，结果提前5天完成任务．求原来每天改造道路多少米？
已知一次函数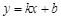
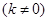与反比例函数
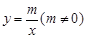的图象交于A（2，3）， B（-6，n） 两点．
（1）求一次函数和反比例函数的解析式；
（2）P是y轴上一点，且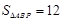
，直接写出P点坐标．
已知
，求代数式
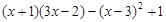的值．