列方程或方程组解应用题:
某工程队改造一条长2 500米的道路.在改造了1 000米后,为了减少施工对交通造成的影响,采用了新的施工工艺,使每天的工作效率是原来的1.5倍,结果提前5天完成任务.求原来每天改造道路多少米?
应用题
甲、乙两辆车在一条公路上匀速行驶,为了确定汽车的位置.我们用OX表示这条公路,原点O为零千米路标,并作如下约定:速度为正,表示汽车向数轴的正方向行驶;速度为负,表示汽车向数轴的负方向行驶;速度为零,表示汽车静止.行程为正,表示汽车位于零千米的右侧;行程为负,表示汽车位于零千米的左侧:行程为零,表示汽车位于零千米处.
(1)根据题意,填写下列表格;
| 时间(h) |
0 |
5 |
7 |
x |
| 甲车位置(km) |
190 |
-10 |
||
| 乙车位置(km) |
170 |
270 |
(2)甲、乙两车能否相遇,如果相遇,求相遇时的时刻及在公路上的位置;如果不能相遇,请说明理由;
(3)甲、乙汽车能否相距90km,如果能,求相距90 km的时刻及其位置;如不能,请说明理由.
观察图,解答下列问题.
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,……,第六层有11个圆圈.如果要你继续画下去第n层 有 圆圈
(2)某一层上有65个圆圈,这是第 层
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3 = 22.
同样,
由前三层的圆圈个数和得:1+3+5 = 32.
由前四层的圆圈个数和得:1+3+5+7 = 42.
由前五层的圆圈个数和得:1+3+5+7+9 = 52.
……
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)计算:1+3+5+…+299的和;
(5)计算:101+103+105+…+299的和.
某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
+6 |
-2 |
-4 |
+12 |
-10 |
+16 |
-8 |
(1)根据记录的数据可知该厂星期四生产自行车 辆;
(2)根据记录的数据可知该厂本周实际生产自行车 辆;
(3)产量最多的一天比产量最少的一天多生产自行车 辆;
(4)该厂实行每周计件工资制,每生产一辆车可得30元,若超额完成任务,则超过部分每辆另奖25元,那么该厂工人这一周的工资总额是多少元?
有理数 、
、 、
、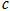 在数轴上的位置如图,
在数轴上的位置如图,
(1)判断正负,用“>”或“<”填空:c-b 0,a+b 0,a-c 0.
(2)化简:|c-b|+|a+b|-|a-c|.
已知代数式A=2x2+3xy+2y-1,B=x2-xy+x-
(1)求A-2B;
(2)若A-2B的值与x的取值无关,求y的值.