某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为：
，且物价部门规定这种绿茶的销售单价不得高于90元/千克．设这种绿茶在这段时间内的销售利润为y（元），解答下列问题：
（1）求出y与x之间的函数关系式；
（2）当x取何值时，y的值最大？最大值为多少？
（3）如果公司想要在这段时间内获得2250元的销售利润，销售单价应定为多少元？
如图1，正方形ABCD中，点H在BC上，连接DH交正方形对角线AC于点E，过点E作DH的垂线交线段AB、CD于点F、G。
（1）求证：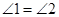
（2）判断DH、FG的数量关系，并说明理由；
（3）在图1中，延长FG与BC交于点P，连接DF、DP（如图2），试探究DF与DP的关系，并说明理由。
如图，已知一个边长分别为6、8、10的直角三角形，请设计出一个有一条边长为8的直角三角形，使这两个直角三角形能够拼成一个等腰三角形。
（1）画出4种不同拼法（周长不等）的等腰三角形；
（2）求出4种不同拼法的图形的等腰三角形的周长。
如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线于点F。
（1）找出图中与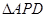
全等的三角形，并说明理由；
（2）猜想三条线段PC、PE、PF之间的比例关系，并说明理由。
课堂上对关于x的方程：
的解进行合作探究时，甲同学发现，当m=0时，方程的两根都为1，当m>0时，方程有两个不相等的实数根；乙同学发现，无论m取什么正实数时方程的两根都不可能相等；丙同学发现无论m取什么正实数时方程的两根这和均为定值。
（1）请找一个m的值代入方程使方程的两个根为互不相等的整数，并求这两个根；
（2）请选择乙或丙同学的发现加以判断，并说明理由。
如图，把两块含有300的相同的直角三角尺按如图所示摆放，使点C、B、E在同一直线上，连接CD。
（1）求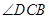
的度数
（2）若AC=6cm，求
的面积。