已知函数 ,
,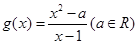 .
.
(1)求函数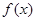 的单调增区间;
的单调增区间;
(2)若 ,解不等式
,解不等式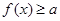 ;
;
(3)若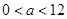 ,且对任意
,且对任意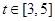 ,方程
,方程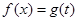 在
在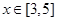 总存在两不相等的实数根,求
总存在两不相等的实数根,求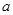 的取值范围.
的取值范围.
【2015高考新课标2,理21】
设函数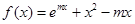 .
.
(Ⅰ)证明: 在
在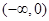 单调递减,在
单调递减,在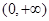 单调递增;
单调递增;
(Ⅱ)若对于任意 ,都有
,都有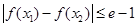 ,求
,求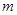 的取值范围.
的取值范围.
【2015高考上海,理23】对于定义域为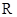 的函数
的函数 ,若存在正常数
,若存在正常数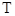 ,使得
,使得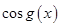 是以
是以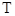 为周期的函数,则称
为周期的函数,则称 为余弦周期函数,且称
为余弦周期函数,且称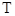 为其余弦周期.已知
为其余弦周期.已知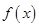 是以
是以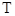 为余弦周期的余弦周期函数,其值域为
为余弦周期的余弦周期函数,其值域为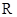 .设
.设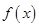 单调递增,
单调递增, ,
, .
.
(1)验证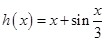 是以
是以 为周期的余弦周期函数;
为周期的余弦周期函数;
(2)设 .证明对任意
.证明对任意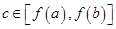 ,存在
,存在 ,使得
,使得 ;
;
(3)证明:“ 为方程
为方程 在
在 上得解”的充要条件是“
上得解”的充要条件是“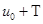 为方程
为方程 在
在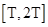 上有解”,并证明对任意
上有解”,并证明对任意 都有
都有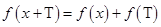 .
.
【2015高考北京,理20】已知数列 满足:
满足: ,
, ,且
,且
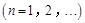 .
.
记集合 .
.
(Ⅰ)若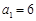 ,写出集合
,写出集合 的所有元素;
的所有元素;
(Ⅱ)若集合 存在一个元素是3的倍数,证明:
存在一个元素是3的倍数,证明: 的所有元素都是3的倍数;
的所有元素都是3的倍数;
(Ⅲ)求集合 的元素个数的最大值.
的元素个数的最大值.
【2015江苏高考,23】(本小题满分10分)已知集合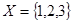 ,
, ,
,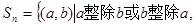
 ,令
,令 表示集合
表示集合 所含元素的个数.
所含元素的个数.
(1)写出 的值;
的值;
(2)当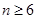 时,写出
时,写出 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
【2015高考湖南,理18】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.