在平面直角坐标系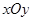 中,椭圆
中,椭圆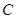 的中心为原点,焦点
的中心为原点,焦点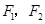 在
在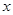 轴上,离心率为
轴上,离心率为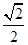 ,过点
,过点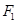 的直线
的直线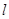 交椭圆
交椭圆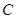 于
于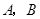 两点,且
两点,且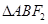 的周长为16,求椭圆
的周长为16,求椭圆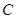 的标准方程.
的标准方程.
 的取值范围为[0,10],给出如图所示程序框图,输入一个数
的取值范围为[0,10],给出如图所示程序框图,输入一个数 .
.
(1)请写出程序框图所表示的函数表达式;
(2)求输出的 (
( )的概率;
)的概率;
(3)求输出的 的概率.
的概率.
从某学校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的条形图.
(1)根据已知条件填写下面表格:
| 组别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 频数 |
(2)估计这所学校高三年级800名学生中身高在175cm以上(含175cm)的人数;
(3)在样本中,若第二组有1人为男生,其余为女生,第七组有1人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为同性别学生的概率是多少?
已知 ,
, ,
, 是一个平面内的三个向量,其中
是一个平面内的三个向量,其中 =(1,3).
=(1,3).
(1)若| |=2
|=2 ,
, ∥
∥ ,求
,求 及
及 ;
;
(2)若| |=
|= ,且
,且 -3
-3 与2
与2 +
+ 垂直,求
垂直,求 与
与 的夹角.
的夹角.
已知函数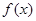 =-
=-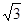 cos2x+2cos2(
cos2x+2cos2(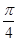 -x)-1.
-x)-1.
(1)求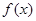 的最小正周期;
的最小正周期;
(2)求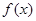 在区间[-
在区间[-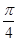 ,
,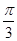 ]上的取值范围.
]上的取值范围.
已知角 的顶点与原点重合,始边与x轴的非负半轴重合,而终边经过点P(1,-2)..
的顶点与原点重合,始边与x轴的非负半轴重合,而终边经过点P(1,-2)..
(1)求tan 的值;
的值;
(2)求 的值.
的值.