在△ABC中，角A，B，C的对边分别为a，b，c，且满足
，
．
（1）求△ABC的面积；
（2）若b+c=5，求a的值．
（本小题满分10分）已知圆C经过点
，和直线
相切，且圆心在直线
上．
（Ⅰ）求圆C的方程；
（Ⅱ）已知直线l经过原点，并且被圆C截得的弦长为2，求直线l的方程．
（本小题满分9分）如图，四棱锥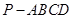
的底面是正方形，
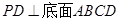，点E为PB的中点. 且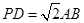
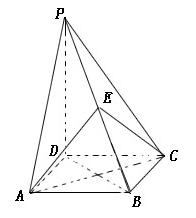
（1）求证：平面
；
（2）求AE与平面PDB所成的角的大小.
（本小题满分8分）直线l过点P（4,1），
（1）若直线l过点Q（－1,6），求直线l的方程；
（2）若直线l在y轴上的截距是在x轴上的截距的2倍，求直线l的方程．
（本小题满分10分）已知圆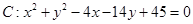
及点
.
（1）若
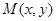为圆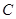
上任一点，求
的最大值和最小值；
（2）已知点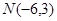
，直线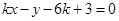
与圆C交于点A、B， 当
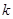为何值时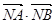
取到最小值。
（本小题满分10分）已知直角梯形ABCD和矩形CDEF所在的平面互相垂直，
//
（1）证明：
（2）设二面角
的平面角为
,求
；
（3）M为AD的中点，在DE上是否存在一点P，使得MP//平面BCE？若存在，求出DP的长；若不存在，请说明理由。