已知数列 是递增的等比数列,满足
是递增的等比数列,满足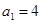 ,且
,且 是
是 .
.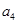 的等差中项,数列
的等差中项,数列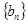 满足
满足 ,其前n项和为
,其前n项和为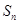 ,且
,且 .
.
(1)求数列 ,
,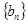 的通项公式;
的通项公式;
(2)数列 的前n项和为
的前n项和为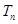 ,若不等式
,若不等式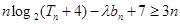 对一切
对一切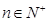 恒成立,求实数
恒成立,求实数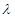 的取值范围.
的取值范围.
在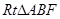 中,AB=2BF=4,C,E分别是AB,AF的中点(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.
中,AB=2BF=4,C,E分别是AB,AF的中点(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.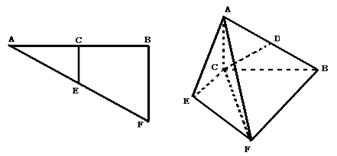
(1)求证:CD∥平面AEF;
(2)求证:平面AEF⊥平面ABF;
(3)求三棱锥C-AEF的体积,
某公司研制出一种新型药品,为测试该药品的有效性,公司选定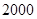 个药品样本分成三组,测试结果如下表:
个药品样本分成三组,测试结果如下表:
| 分组 |
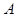 组 组 |
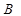 组 组 |
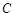 组 组 |
| 药品有效 |
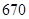 |
 |
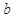 |
| 药品无效 |
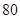 |
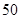 |
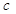 |
已知在全体样本中随机抽取 个,抽到
个,抽到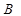 组药品有效的概率是
组药品有效的概率是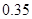 .
.
(1)现用分层抽样的方法在全体样本中抽取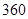 个测试结果,问应在
个测试结果,问应在 组抽取样本多少个?
组抽取样本多少个?
(2)已知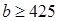 ,
,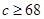 ,求该药品通过测试的概率(说明:若药品有效的概率不小于
,求该药品通过测试的概率(说明:若药品有效的概率不小于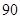 %,则认为测试通过).
%,则认为测试通过).
数列 的前n项和记为
的前n项和记为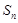 ,
,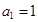 ,点
,点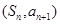 在直线
在直线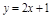 上,n∈N*.
上,n∈N*.
(1)求证:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式
的通项公式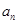 ;
;
(2)设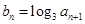 ,
,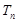 是数列
是数列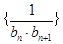 的前n项和,求
的前n项和,求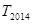 的值.
的值.
在 中,角A,B,C所对边分别为a,b,c,且向量
中,角A,B,C所对边分别为a,b,c,且向量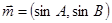 ,
,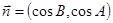 ,满足
,满足
(1)求角C的大小;
(2)若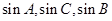 成等差数列,且
成等差数列,且 ,求边
,求边 的长
的长
已知函数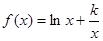 ,
, .
.
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若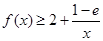 恒成立,求实数
恒成立,求实数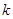 的取值范围;
的取值范围;
(3)设 ,若对任意的两个实数
,若对任意的两个实数 满足
满足 ,总存在
,总存在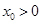 ,使得
,使得
 成立,证明:
成立,证明: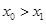 .
.