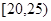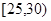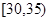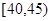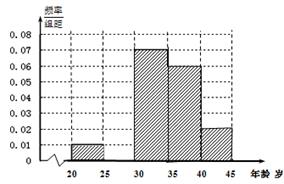
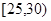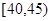电影院为了解观看此部电影的观众年龄的情况，在某场次的100名观众中随机调查了20名观众，已知抽到的观众年龄可分成5组：，，，，，根据调查结果得出年龄情况残缺的频率分布直方图如下图所示。（1）根据已知条件，补充画完整频率分布直方图，并估计该电影院观看此部电影的观众年龄的平均数；（2）现在从年龄属于和的两组中随机抽取2人，求他们属于同一年龄组的概率。
设数列的前项和，数列满足． （1）求数列的通项公式； （2）求数列的前项和．
如图，在中，是边的中点，且，． （1）求的值； （2）求的值．
已知是公差不为零的等差数列，，且成等比数列． （1）求数列的通项公式； （2）求数列的前项和．
（1）已知x<，求函数y＝4x－2＋的最大值； （2）已知x>0，y>0且＝1，求x＋y的最小值．
已知=，=，=，设是直线上一点，是坐标原点， （1）求使取最小值时的； （2）对（1）中的点，求的余弦值。
试卷网 试题网 古诗词网 作文网 范文网
Copyright ©2020-2025 优题课 youtike.com 版权所有
粤ICP备20024846号
，
，
，
，
，根据调查结果得出年龄情况残缺的频率分布直方图如下图所示。
和的两组中随机抽取2人，求他们属于同一年龄组的概率。
的前
项和
，数列
满足
．
．
中，
是边
的中点，且
，
．
的值；
的值．
是公差不为零的等差数列，
，且
成等比数列．
的前
项和
．
，求函数y＝4x－2＋
的最大值；
＝1，求x＋y的最小值．
=
，
=
，
=
，设
是直线
上一点，
是坐标原点，
取最小值时的
； 
的余弦值。