某河流上的一座水力发电站,每年六月份的发电量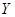 (单位:万千瓦时)与该河上游在六月份的降雨量
(单位:万千瓦时)与该河上游在六月份的降雨量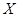 (单位:毫米)有关据统计,当
(单位:毫米)有关据统计,当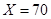 时,
时, ;
;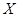 每增加10,
每增加10,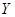 增加5.已知近20年
增加5.已知近20年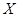 的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(1)完成如下的频率分布表:近20年六月份降雨量频率分布表
(2)假定今年六月份的降雨量与近20年六月份降雨量的分布规律相同,并将频率视为概率,求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
已知椭圆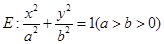 的左右焦点为
的左右焦点为 ,过点
,过点 且斜率为正数的直线
且斜率为正数的直线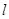 交椭圆
交椭圆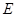 于
于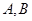 两点,且
两点,且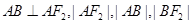 成等差数列。
成等差数列。
(1)求椭圆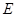 的离心率;
的离心率;
(2)若直线 与椭圆
与椭圆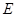 交于
交于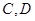 两点,求使四边形
两点,求使四边形 的面积最大时的
的面积最大时的 值。
值。
设函数 ,已知
,已知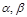 不论为何实数时,恒有
不论为何实数时,恒有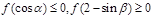 ,对于正数数列
,对于正数数列 ,其前项和
,其前项和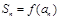 (
( )
)
(1)求 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)是否存在等比数列 ,使得
,使得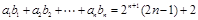 对一切正整数
对一切正整数 都成立,并证明你的结论;
都成立,并证明你的结论;
(4)若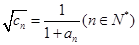 ,且数列
,且数列 的前
的前 项和为
项和为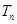 ,比较
,比较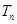 与
与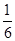 的大小。
的大小。
如图,已知正方形 的边长为1,
的边长为1, 平面
平面 ,
,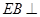 平面
平面 ,
,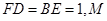 为
为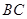 边上的动点。
边上的动点。
(1)证明: 平面
平面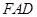 ;
;
(2)试探究点 的位置,使平面
的位置,使平面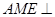 平面
平面 。
。
已知函数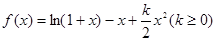 。
。
(1)当 时,求曲线
时,求曲线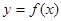 在点
在点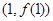 处的切线方程;
处的切线方程;
(2)求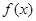 的单调区间。
的单调区间。
某汽车驾驶学校在学员学习完毕后,对学员的驾驶技术进行9选3考试(即共9项测试,随机选取3项)考核,若全部过关,则颁发结业证;若不合格,则参加下期考核,直至合格为止,若学员小李抽到“移库”一项,则第一次合格的概率为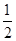 ,第二次合格的概率为
,第二次合格的概率为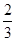 ,第三次合格的概率为
,第三次合格的概率为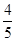 ,若第四次抽到可要求调换项目,其它选项小李均可一次性通过。
,若第四次抽到可要求调换项目,其它选项小李均可一次性通过。
(1)求小李第一次考试即通过的概率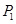 ;
;
(2)求小李参加考核的次数 的分布列和数学期望。
的分布列和数学期望。