设 分别是椭圆
分别是椭圆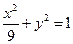 的左右焦点.
的左右焦点.
(1)若M是该椭圆上的一个动点,求 的最大值和最小值;
的最大值和最小值;
(2)设过定点(0,2)的直线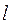 与椭圆交于不同的两点A、B,且
与椭圆交于不同的两点A、B,且
 为钝角,(其中O为坐标原点),求直线
为钝角,(其中O为坐标原点),求直线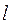 的余斜率
的余斜率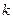 的取值范围。
的取值范围。
两定点的坐标分别A(-1,0),B(2,0),动点M满足条件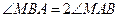 ,求动点M的轨迹方程并指出轨迹是什么图形.
,求动点M的轨迹方程并指出轨迹是什么图形.
直线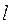 与抛物线
与抛物线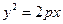 (
( p
p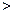 0)交于A、B两点,且
0)交于A、B两点,且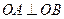 (O为坐标原点),求证:
(O为坐标原点),求证:
(1)A、B两点的横坐标之积,纵坐标之积都是常数; (2)直线AB经过x轴上一个定点.
(2)直线AB经过x轴上一个定点.
某单位建造一间地面面积为12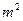 的背面靠墙的矩形小屋,房屋正面的造价为12
的背面靠墙的矩形小屋,房屋正面的造价为12 00元/
00元/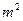 ,房屋侧面造价为800元/
,房屋侧面造价为800元/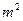 ,屋顶
,屋顶 的总造价为5800元,如果墙面高为3m,且不计房屋背面费用,问怎样设计房屋能使得总造价最低,最低造价为多少元?
的总造价为5800元,如果墙面高为3m,且不计房屋背面费用,问怎样设计房屋能使得总造价最低,最低造价为多少元?
12分)已知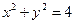 ,
,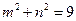 ,求
,求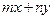 的范围。
的范围。