如图,四边形 内接于⊙
内接于⊙ ,过点
,过点 作⊙
作⊙ 的切线
的切线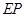 交
交 的延长线于
的延长线于 ,已知
,已知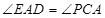 .
.
证明:(1) ;
;
(2) .
.
(本小题满分12分)已知椭圆与双曲线 的焦点相同,且它们的离心率之和等于
的焦点相同,且它们的离心率之和等于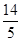 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)过椭圆内一点 作一条弦
作一条弦 ,使该弦被点
,使该弦被点 平分,求弦
平分,求弦 所在直线方程.
所在直线方程.
(本小题满分12分)在 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求△
,求△ 的面积.
的面积.
(本小题满分12分)已知 为复数,
为复数, 和
和 均为实数,其中
均为实数,其中 是虚数单位.
是虚数单位.
(Ⅰ)求复数 和
和 ;
;
(Ⅱ)若 在第四象限,求
在第四象限,求 的范围.
的范围.
(本小题满分14分)已知椭圆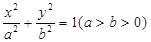 上的点
上的点 到左右两焦点
到左右两焦点 的距离之和为
的距离之和为 ,离心率为
,离心率为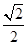 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过右焦点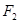 的直线
的直线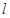 交椭圆于
交椭圆于 两点.
两点.
(1)若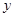 轴上一点
轴上一点 满足
满足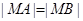 ,求直线
,求直线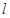 斜率
斜率 的值;
的值;
(2)是否存在这样的直线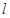 ,使
,使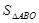 的最大值为
的最大值为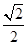 (其中
(其中 为坐标原点)?若存在,求直线
为坐标原点)?若存在,求直线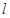 方程;若不存在,说明理由.
方程;若不存在,说明理由.
(本小题满分13分)已知数列 的前
的前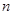 项和
项和 ,满足
,满足 为常数,且
为常数,且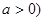 ,且
,且 是
是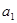 与
与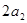 的等差中项.
的等差中项.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列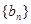 的前
的前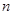 项和
项和 .
.