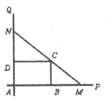
如下图,互相垂直的两条公路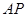 、
、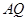 旁有一矩形花园
旁有一矩形花园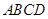 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园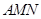 ,要求点
,要求点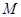 在射线
在射线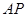 上,点N在射线
上,点N在射线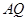 上,且直线
上,且直线 过点
过点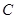 ,其中
,其中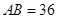 米,
米,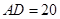 米.记三角形花园
米.记三角形花园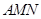 的面积为
的面积为 .
.
(1)问: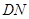 取何值时,
取何值时, 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(2)若 不超过1764平方米,求
不超过1764平方米,求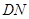 长的取值范围.
长的取值范围.
(本小题满分14分)
在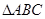 中,
中,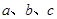 分别为内角
分别为内角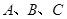 的对边,
的对边,
且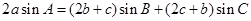
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若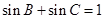 ,试判断
,试判断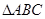 的形状.
的形状.
(本题满分14分)已知数列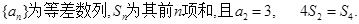
(Ⅰ)求数列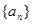 的通项公式;
的通项公式;
(Ⅱ)求证数列 是等比数列;
是等比数列;
(Ⅲ)求使得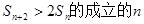 的集合。
的集合。
(本题满分14分)
某企业准备投资1200万元兴办一所中学,对当地教育市场进行调查后,得到了如下的数据表格(以班级为单位):
| 学段 |
硬件建设(万元) |
配备教师数 |
教师年薪(万元) |
| 初中 |
26 / 班 |
2 / 班 |
2 / 人 |
| 高中 |
54 / 班 |
3 / 班 |
2 / 人 |
因生源和环境等因素,全校总班级至少20个班,至多30个班。
(Ⅰ)请用数学关系式表示上述的限制条件;(设开设初中班x个,高中班y个)
(Ⅱ)若每开设一个初、高中班,可分别获得年利润2万元、3万元,请你合理规划办学规模使年利润最大,最大为多少?
 的三边,其面积
的三边,其面积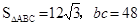 ,角A为锐角
,角A为锐角
(Ⅰ) 求角A;
(Ⅱ)已知b+c=14,求边长a.
已知不等式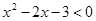 的解集是A,不等式
的解集是A,不等式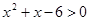 的解集是B,若不等式
的解集是B,若不等式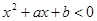 的解集是
的解集是 ,则:
,则:
(1)求 A, B, ;
;
(2)求 。
。