如图，
的外接圆的切线AE与BC的延长线相交于点E，
的平分线与BC相交于点D，求证：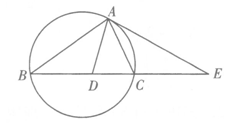
（1）
；
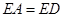（2）
．
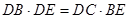如图，在平面直角坐标系xOy中，椭圆C：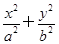
＝1(a＞b＞0)的离心率为
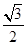，以原点为圆心，椭圆C的短半轴长为半径的圆与直线x－y＋2＝0相切．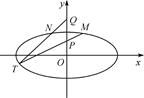
(1)求椭圆C的方程；
(2)已知点P(0，1)，Q(0，2)．设M、N是椭圆C上关于y轴对称的不同两点，直线PM与QN相交于点T，求证：点T在椭圆C上．
已知椭圆C：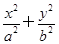
＝1(a＞b＞0)的离心率为
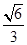，F为椭圆的右焦点，M、N两点在椭圆C上，且
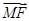＝λ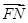
(λ＞0)，定点A(－4，0)．
(1)求证：当λ＝1时，
⊥
；
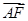(2)若当λ＝1时，有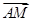
·
＝
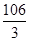，求椭圆C的方程．.
椭圆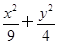
＝1的焦点为F1、F2，点P为椭圆上的动点，当∠F1PF2为钝角时，求点P的横坐标x0的取值范围．
若椭圆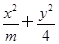
＝1的焦距为2，求椭圆上的一点到两个焦点的距离之和．
根据下列条件求椭圆的标准方程：
(1)两准线间的距离为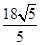
，焦距为2
；
(2)已知P点在以坐标轴为对称轴的椭圆上，点P到两焦点的距离分别为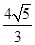
和
，过P点作长轴的垂线恰好过椭圆的一个焦点．