已知:b是最小的正整数,且a、b满足 =0,请回答问题
=0,请回答问题
(1)请直接写出a、b、c的值。
a=__________; b=__________;c=__________
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子: (请写出化简过程)
(请写出化简过程)
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB。请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
阅读理解:
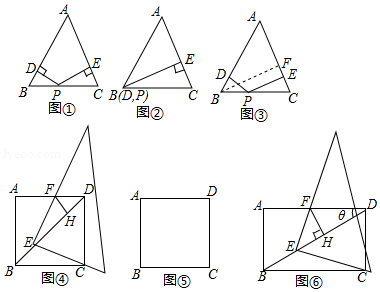
问题:我们在研究“等腰三角形底边上的任意一点到两腰的距离和为定值”时,如图①,在 中, ,点 为底边 上的任意一点, 于点 , 于点 ,求证: 是定值,在这个问题中,我们是如何找到这一定值的呢?
思路:我们可以将底边 上的任意一点 移动到特殊的位置,如图②,将点 移动到底边的端点 处,这样,点 、 都与点 重合,此时, , ,这样 .因此,在证明这一命题时,我们可以过点 作 边上的高 (如图③ ,证明 即可.
请利用上述探索定值问题的思路,解决下列问题:
如图④,在正方形 中,一直角三角板的直角顶点 在对角线 上运动,一条直角边始终经过点 ,另一条直角边与射线 相交于点 ,过点 作 ,垂足为 .
(1)试猜想 与 的数量关系,并加以证明;
(2)当点 在 的延长线上运动时, 与 之间存在怎样的数量关系?请在图⑤中画出图形并直接写出结论;
(3)如图⑥所示,如果将正方形 改为矩形 , ,其它条件不变,请直接写出 与 的数量关系.
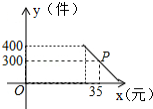
某商店购进一批进价为20元 件的日用商品,第一个月,按进价提高 的价格出售,售出400件,第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量 (件 与销售单价 (元 的关系如图所示.
(1)图中点 所表示的实际意义是 ;销售单价每提高1元时,销售量相应减少 件;
(2)请直接写出 与 之间的函数表达式 ;自变量 的取值范围为 ;
(3)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
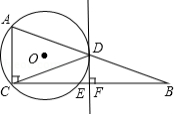
如图,已知 , , ,点 为 的中点,过点 作 的垂线,垂足为点 ,过点 、 、 作 交 于点 ,连接 、 .
(1)求证: 为 的切线;
(2)若 , ,求 的长.
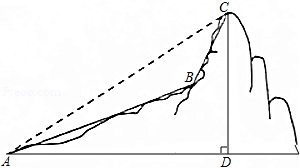
“五 一”期间,小亮与家人到某旅游风景区登山,他们沿着坡度为 的山坡 向上走了1300米,到达缆车站 处,乘坐缆车到达山顶 处,已知点 、 、 、 在同一平面内,从山脚 处看山顶 处的仰角为 ,缆车行驶路线 与水平面的夹角为 ,求山高 .(结果精确到1米,
(注 坡度是指坡面的铅直高度与水平宽度的比)
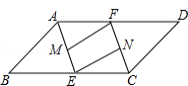
如图,在 中, 和 的平分线 、 分别交 、 于点 、 ,点 、 分别为 、 的中点,连接 、 ,试判断 和 的数量关系和位置关系,并加以证明.