已知抛物线
(1)填空:抛物线的顶点坐标是( , ),对称轴是 ;
(2)已知y轴上一点A(0,-2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点N,使以点O、点A、点M、点N为顶点的四边形为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.

如图, 是⊙O的直径,弦BC=5,∠BOC=60°,OE⊥AC,垂足为E.
是⊙O的直径,弦BC=5,∠BOC=60°,OE⊥AC,垂足为E.
(1)求OE的长;
(2)求劣弧AC的长.
已知二次函数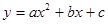 的图象与x 轴交于(2,0)、(4,0),顶点到x 轴的距离为3,求函数的解析式。
的图象与x 轴交于(2,0)、(4,0),顶点到x 轴的距离为3,求函数的解析式。
以直线 为对称轴的抛物线过点(3,0),(0,3),求此抛物线的解析式.
为对称轴的抛物线过点(3,0),(0,3),求此抛物线的解析式.
已知抛物线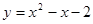 。
。<1>求抛物线顶点M的坐标;
<2>若抛物线与x轴的交点分别为点A、B(点A在点B的左边),与y轴交于点C,点N为线段BM上的一点,过点N作x轴的垂线,垂足为点Q.当点N在线段BM上运动时(点N不与点B,点M重合),设NQ的长为t,四边形NQAC的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
<3>在对称轴右侧的抛物线上是否存在点P,使△PAC为直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
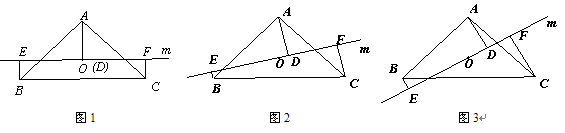
我们知道三角形三条中线的交点叫做三角形的重心.经过证明我们可得三角形重心具备下面的性质: 重心到顶点的距离与重心到该顶点对边中点的距离之比为2﹕1.请你用此性质解决下面的问题.
已知:如图,点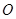 为等腰直角三角形
为等腰直角三角形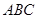 的重心,
的重心,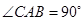 ,直线
,直线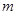 过点
过点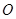 ,过
,过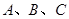 三点分别作直线
三点分别作直线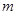 的垂线,垂足分别为点
的垂线,垂足分别为点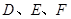 .
.
<1>当直线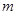 与
与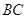 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段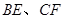 和
和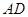 三者之间的数量关系并证明;
三者之间的数量关系并证明;
<2>当直线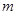 绕点
绕点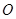 旋转到与
旋转到与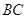 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段
不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段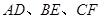 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.