(本小题满分10分)
已知:函数
(1)若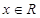 ,求函数
,求函数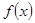 的最小正周期及图像的对称轴方程;
的最小正周期及图像的对称轴方程;
(2)设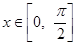 ,
,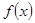 的最小值是-2,最大值是
的最小值是-2,最大值是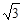 ,求:实数
,求:实数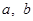 的值。
的值。
(本小题满分6分)
已知:如图,两个长度为1的平面向量 ,它们的夹角为
,它们的夹角为 ,点C是以O为圆心的劣弧
,点C是以O为圆心的劣弧 的中点。
的中点。
求:(1) 的值;(2)
的值;(2) 的值。
的值。
设二次函数 的图象以
的图象以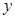 轴
轴 为对称轴,已知
为对称轴,已知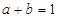 ,而且若点
,而且若点 在
在 的图象上,则点
的图象上,则点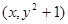 在函数
在函数 的图象上
的图象上
(1)求 的解析式
的解析式
(2)设 ,问是否存在实数
,问是否存在实数 ,使
,使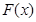 在
在 内是减函数,在
内是减函数,在 内是增函数。
内是增函数。
已知定义在R上的函数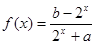 是奇函数
是奇函数
(1)求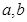 的值;
的值;
(2)判断 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;
(3)若对任意的 ,不等式
,不等式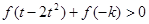 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知 是定义在
是定义在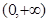 上的增函数,且满足
上的增函数,且满足 ,
, 。
。
(1)求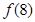
(2)求不等式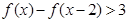 的解集
的解集