已知定义在R上的函数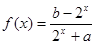 是奇函数
是奇函数
(1)求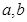 的值;
的值;
(2)判断 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;
(3)若对任意的 ,不等式
,不等式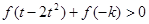 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知二次函数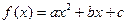
(1)若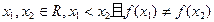
求证:关于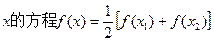 有两个不相等的实根,且必有一个根属于
有两个不相等的实根,且必有一个根属于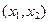
(2)若关于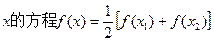 在
在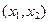 的根为m,且
的根为m,且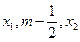 成等差数例,设函数
成等差数例,设函数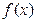 的图象的对称轴为
的图象的对称轴为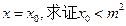 。
。
已知点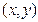 在椭圆
在椭圆 的第一象限上运动
的第一象限上运动
(1)求点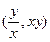 的轨迹
的轨迹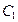 的方程
的方程
(2)若把轨迹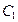 的方程表达式认为
的方程表达式认为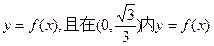 有最大值,试求椭圆
有最大值,试求椭圆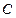 的离心率的取值范围。
的离心率的取值范围。
已知数例 的首项
的首项 ,前n项和
,前n项和
(1)求通项 ;(2)记
;(2)记 为数例
为数例 的前
的前 项和,求证
项和,求证
已知六条桥梁横跨A、B两岸,假设各条桥梁的车流量分别为1,1,2,2,3,4(单位万辆),现从这六条桥梁中任取三条桥梁,考察这三条桥梁的车流量之和
(1)求 的概率(2)求
的概率(2)求 的概率(3)求
的概率(3)求 的数学期望
的数学期望
已知正三棱柱 的各棱长都为
的各棱长都为 ,P为
,P为 上的点,
上的点,
(1)若 ,求
,求 的值,使
的值,使
(2)若 ,求二面角
,求二面角 的大小
的大小