(10分)选修4-1:几何证明选讲.
已知C点在圆O直径BE的延长线上,CA切圆O于A点,DC是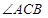 的平分线交AE于点F,交AB于D点.
的平分线交AE于点F,交AB于D点.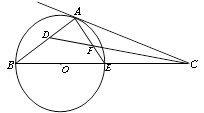
(1) 求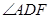 的度数;
的度数;
(2) 若AB=AC,求AC:BC.
(10分)某市为了发展农村贫困教育,市教育局决定从5位优秀骨干教师(2位女教师,3位男教师)中选派3位教师担任下乡支教教师.
(1) 选派的三位教师中恰有2位女教师的概率;
(2) 选派的三位教师中至少有1位女教师的概率;
(10分)已知圆 :
: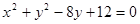 ,和定点
,和定点 ,
,
求:(1) 过点 作圆
作圆 的切线
的切线 ,求直线
,求直线 方程;
方程;
(2) 过点 作直线
作直线 与圆
与圆 相交于
相交于 、
、 两点,且
两点,且 时,求直线
时,求直线 的方程.
的方程.
(10)分) 已知正方体 ,
, 是底
是底 对角线的交点.
对角线的交点.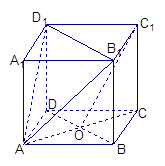
求证:(1)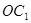 ∥面
∥面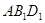 ;(2)
;(2) 面
面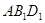 .
.
(10分)设 ,
, 求
求 的值.
的值.