在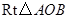 中,
中,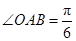 ,斜边
,斜边 .
.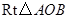 以直线
以直线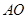 为轴旋转得到
为轴旋转得到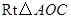 ,且二面角
,且二面角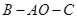 是直二面角,动点
是直二面角,动点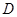 在斜边
在斜边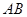 上。
上。
(1)求证:平面 平面
平面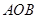 ;
;
(2)当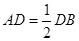 时,求异面直线
时,求异面直线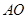 与
与 所成角的正切值;
所成角的正切值;
(3)求 与平面
与平面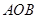 所成最大角的正切值.
所成最大角的正切值.
记关于x的不 等式
等式 的解集为P,不等式(x-1)2≤1的解集为Q.
的解集为P,不等式(x-1)2≤1的解集为Q.
(Ⅰ)若 ,求P;
,求P;
(Ⅱ)若Q P,求正数a的取值范围.
P,求正数a的取值范围.
已知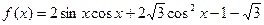 ,
,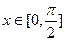
(Ⅰ) 求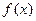 的最大值及此时
的最大值及此时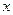 的值;
的值;
(Ⅱ) 求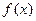 在定义域上的单调递增区间。
在定义域上的单调递增区间。
已知函数 图像上点
图像上点 处的切线与直线
处的切线与直线
平行(其中 ),
),
(I)求函数 的解析式;
的解析式;
(II)求函数 上的最小值;
上的最小值;
(III)对一切 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式 ,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出
,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出 该商品11千克。(I)
该商品11千克。(I) 求a的值;
求a的值;
(II)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大。
在△ABC中,a,b,c分别为角A,B,C的对边,设 f(x)=a2x2-(a2-b2)x-4c2.
(1)若 f(1)=0,且B-C= ,求角C;
,求角C;
(2)若 f(2)=0,求角C的取值范围.