17.有甲乙两个班级进行数学考 试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
| |
优秀 |
非优秀 |
总计 |
| 甲班 |
10 |
|
|
| 乙班 |
|
30 |
|
| 合计 |
|
|
105 |
已知在全部105人中抽到随机抽取2人为优秀的概率为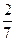
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成 绩与班级有关系”。
绩与班级有关系”。
(3)若按下面的方法从甲班优秀的学生抽取一人;把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取的人的序号,试求抽到6或10的概率。
某大型企业人力资源部为了研究企业员工工作积极性和对企业改革态度的关系,随机抽取了189名员工进行调查,所得数据如下表所示
| 积极支持企业改革 |
不赞成企业改革 |
合计 |
|
| 工作积极 |
54 |
40 |
94 |
| 工作一般 |
32 |
63 |
95 |
| 合计 |
86 |
103 |
189 |
对于人力资源部的研究项目,根据上述数据能得出什么结论?
如图,三角形ABC中,AC=BC=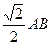 ,ABED是边长为
,ABED是边长为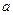 的正方形,平面ABED⊥底面ABC,且,若G、F分别是EC、BD的中点,
的正方形,平面ABED⊥底面ABC,且,若G、F分别是EC、BD的中点,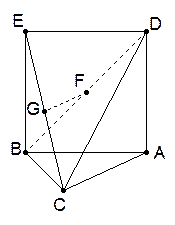
(Ⅰ)求证:GF//底面ABC;
(Ⅱ)求证:平面EBC⊥平面ACD;
(Ⅲ)求几何体ADEBC的体积V。
.(本小题满分14分)已知直线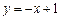 与椭圆
与椭圆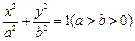 相交于
相交于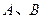 两点,且
两点,且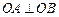 (其中
(其中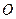 为坐标原点).(1)若椭圆的离心率为
为坐标原点).(1)若椭圆的离心率为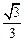 ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)求证:不论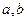 如何变化,椭圆恒过定点
如何变化,椭圆恒过定点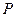
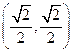 ;
;
(3)若直线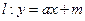 过(2)中的定点
过(2)中的定点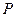 ,且椭圆的离心率
,且椭圆的离心率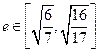 ,求原点到直线
,求原点到直线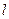 距离的取值范围.
距离的取值范围.
.(本小题满分12分)已知双曲线的两个焦点的坐标为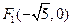 、
、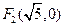 ,离心率
,离心率 .(1)求双曲线的标准方程;(2)设
.(1)求双曲线的标准方程;(2)设 是(1)中所求双曲线上任意一点,过点
是(1)中所求双曲线上任意一点,过点 的直线与两渐近线
的直线与两渐近线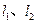 分别交于点
分别交于点 ,若
,若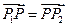 ,求
,求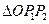 的面积.
的面积.
(本小题满分12分) 如图, 正方体ABCD-A1B1C1D1的棱长为6, 动点M在棱A1B1上. (1) 当M为A1B1的中点时, 求CM与平面DC1所成角的正弦值;
如图, 正方体ABCD-A1B1C1D1的棱长为6, 动点M在棱A1B1上. (1) 当M为A1B1的中点时, 求CM与平面DC1所成角的正弦值;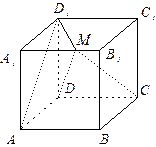
(2) 当A1M=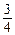 A1B1时, 求点C到平面D1DM的距离.
A1B1时, 求点C到平面D1DM的距离.