设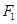 ,
, 分别是椭圆
分别是椭圆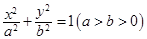 的左右焦点,M是C上一点且
的左右焦点,M是C上一点且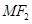 与x轴垂直,直线
与x轴垂直,直线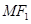 与C的另一个交点为N.
与C的另一个交点为N.
(1)若直线MN的斜率为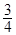 ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且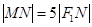 ,求a,b.
,求a,b.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设二面角D-AE-C为60°,AP=1,AD= ,求三棱锥E-ACD的体积.
,求三棱锥E-ACD的体积.
某公司为了解用户对其产品的满意度,从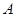 ,
,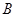 两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
| 满意度评分 |
低于70分 |
70分到89分 |
不低于90分 |
| 满意度等级 |
不满意 |
满意 |
非常满意 |
记时间C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
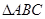 中,
中,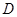 是
是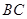 上的点,
上的点,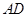 平分
平分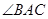 ,
, 面积是
面积是 面积的2倍.
面积的2倍.
(Ⅰ)求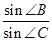 ;
;
(Ⅱ)若 ,
, ,求
,求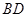 和
和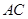 的长.
的长.
选修4-5:不等式选讲
若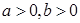 ,且
,且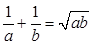 .
.
(Ⅰ)求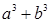 的最小值;
的最小值;
(Ⅱ)是否存在 ,使得
,使得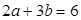 ?并说明理由.
?并说明理由.