平面直角坐标系 中,已知椭圆
中,已知椭圆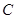 :
: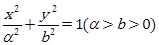 的离心率为
的离心率为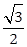 ,且点(
,且点(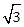 ,
, )在椭圆
)在椭圆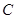 上.
上.
(Ⅰ)求椭圆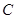 的方程;
的方程;
(Ⅱ)设椭圆 :
: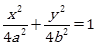 ,
, 为椭圆
为椭圆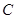 上任意一点,过点
上任意一点,过点 的直线
的直线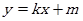 交椭圆
交椭圆 于
于 两点,射线
两点,射线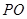 交椭圆
交椭圆 于点
于点 .
.
(i)求 的值;
的值;
(ii)求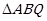 面积的最大值.
面积的最大值.
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
 视觉 视觉 |
视觉记忆能力 |
||||
| 偏低 |
中等 |
偏高 |
超常 |
||
| 听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
| 中等 |
1 |
8 |
3 |
 |
|
| 偏高 |
2 |
 |
0 |
1 |
|
| 超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为 .
.
(I)试确定 、
、 的值;
的值;
(II)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(III)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.
在△ABC中, 为三个内角
为三个内角 为三条边,
为三条边, 且
且
(I)判断△ABC的形状;
(II)若 ,求
,求 的取值范围.
的取值范围.
已知 函数
函数 。
。
(1)求函数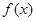 在区间
在区间 上最小值
上最小值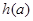 ;
;
(2)对(1)中的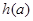 ,若关于
,若关于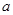 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围;
的取值范围;
(3)若点A ,B
,B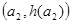 ,C
,C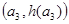 ,从左到右依次是函数
,从左到右依次是函数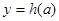 图象上三点,且这三点不共线,求证:
图象上三点,且这三点不共线,求证: 是钝角三角形。
是钝角三角形。
已知中心在原点,焦点在x轴上的椭圆离心率为 ,且经过点
,且经过点 ,过椭圆的左焦点作直线
,过椭圆的左焦点作直线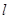 交椭圆于A、B两点,以OA、OB为邻边作平行四边形OAPB。
交椭圆于A、B两点,以OA、OB为邻边作平行四边形OAPB。
(1)求椭圆E的方程
(2)现将椭圆E上的点的纵坐标保持不变,横坐标变为原来的一半,求所得曲线的焦点坐标和离心率
(3)是否存在直线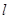 ,使得四边形OAPB为矩形?若存在,求出直线
,使得四边形OAPB为矩形?若存在,求出直线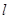 的方程。若不存在,说明理由。
的方程。若不存在,说明理由。
已知数列{ }满足
}满足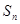 +
+ =2n+1
=2n+1
(1)求出 ,
,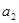 ,
, 的值;
的值;
(2)由(1)猜想出数列{ }的通项公式
}的通项公式 ;
;
(3)用数学归纳法证明(2)的结果.