椭圆 的左、右焦点分别是
的左、右焦点分别是 ,过
,过 斜率为1的直线
斜率为1的直线 与椭圆C相交于A,B两点,且
与椭圆C相交于A,B两点,且 .
.
(1)求椭圆的离心率;
(2)设点 ,
, ,求椭圆C的方程.
,求椭圆C的方程.
两条曲线的极坐标方程分别为 ,它们相交于A,B两点,求线段AB的长.
,它们相交于A,B两点,求线段AB的长.
设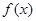 使定义在区间
使定义在区间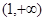 上的函数,其导函数为
上的函数,其导函数为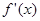 .如果存在实数
.如果存在实数 和函数
和函数 ,其中
,其中 对任意的
对任意的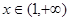 都有
都有 >0,使得
>0,使得 ,则称函数
,则称函数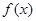 具有性质
具有性质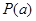 .
.
(1)设函数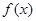
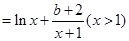 ,其中
,其中 为实数
为实数
①求证:函数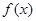 具有性质
具有性质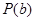 ,②求函数
,②求函数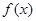 的单调区间.
的单调区间.
(2)已知函数 具有性质
具有性质 ,给定
,给定
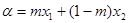 ,
, ,且
,且 ,若|
,若| |<|
|<| |,求
|,求 的取值范围.
的取值范围.
设函数 ,曲线
,曲线 在点(1,
在点(1,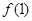 处的切线为
处的切线为 . (Ⅰ)求
. (Ⅰ)求 ;
;
(Ⅱ)证明: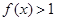 .
.
一走廊拐角处的横截面如图所示,已知内壁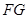 和外壁
和外壁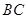 都是半径为1m的四分之一圆弧,
都是半径为1m的四分之一圆弧, 分别与圆弧
分别与圆弧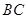 相切于
相切于 两点,
两点, 且两组平行墙壁间的走廊宽度都是1m.
且两组平行墙壁间的走廊宽度都是1m.
(1)若水平放置的木棒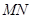 的两个端点
的两个端点 分别在外壁
分别在外壁 和
和 上,且木棒与内壁圆弧相切于点
上,且木棒与内壁圆弧相切于点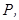 设
设 试用
试用 表示木棒
表示木棒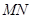 的长度
的长度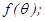
(2)若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值.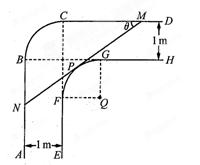
在 中,内角
中,内角 所对的边分别为
所对的边分别为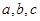 .已知
.已知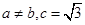 ,
,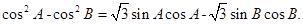
(1)求角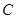 的大小;
的大小;
(2)若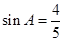 ,求
,求 的面积.
的面积.