已知正方形ABCD的边长为2,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)从C,D,E,F,G,H这六个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求概率P
,求概率P .
.
(2)在正方形ABCD内部随机取一点P,求满足 的概率.
的概率.
已知函数
(1)求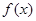 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)已知 是
是 三边长,且
三边长,且 ,
, 的面积
的面积 .求角
.求角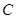 及
及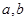 的值.
的值.
已知函数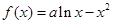 .
.
(1)当 时,求函数
时,求函数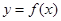 在
在 上的最大值;
上的最大值;
(2)令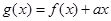 ,若
,若 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(3)当 时,函数
时,函数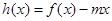 的图像与x轴交于两点
的图像与x轴交于两点 ,且
,且 ,又
,又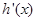 是
是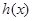 的导函数,若正常数
的导函数,若正常数 满足条件
满足条件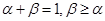 .证明:
.证明: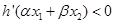 .
.
 的内切圆与三边
的内切圆与三边 的切点分别为
的切点分别为 ,已知
,已知 ,内切圆圆心
,内切圆圆心 ,设点A的轨迹为R.
,设点A的轨迹为R. 
(1)求R的方程;
(2)过点C的动直线m交曲线R于不同的两点M,N,问在x轴上是否存在一定点Q(Q不与C重合),使 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.
如图,正三棱柱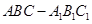 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是 棱的中点,AE交
棱的中点,AE交 于点H.
于点H.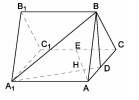
(1)求证: 平面
平面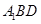 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)求点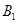 到平面
到平面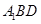 的距离.
的距离.