某商品的进价为每件40元．当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：
（1）若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；
（2）若降价的最小单位为1元，则当降价多少元时，每星期的利润最大？最大利润是多少？
如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等份，每份分别标上1、2、3、4四个数字；转盘B被均匀地分成6等份，每份分别标上1、2、3、4、5、6六个数字。有人为甲、乙两人设计了一个游戏，其规则如下：
（1）同时自由转动转盘A与B；
（2）转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，直到指针停留在某一数字为止），用所指的两个数字作乘积，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，那么乙胜（如转盘A指针指向3，转盘B指针指向5,3×5＝15，按规则乙胜）。
你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并说明理由.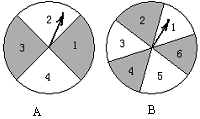
如图，点
在
的直径
的延长线上，点
在上，且AC=CD，∠ACD=120°。
（1）求证：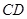
是的切线；
（2）若的半径为2，求图中阴影部分的面积。
作图题：
工人师傅要制作做铁桶，需要在如图中的三角形铁皮上截一个面积最大的圆形铁皮，请作出该圆。（尺规作图，不用说明做法，保留作图痕迹，）
有一人患了流感，经过两轮传染后共有121人患了流感，每轮传染中平均一个人传染了几个人？
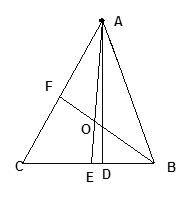
如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=500，∠C=600，求∠DAE和∠BOA的度数。