已知A= ,B=
,B= .
.
(Ⅰ)若
 ,求
,求 的取值范围;
的取值范围;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)己知 、
、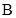 、
、 是椭圆
是椭圆 :
: (
( )上的三点,其中点
)上的三点,其中点 的坐标为
的坐标为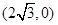 ,
, 过椭圆的中心,且
过椭圆的中心,且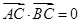 ,
, 。
。
(1)求椭圆 的方程;
的方程;
(2)过点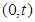 的直线
的直线 (斜率存在时)与椭圆
(斜率存在时)与椭圆 交于两点
交于两点 ,
,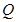 ,设
,设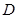 为椭圆
为椭圆 与
与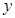 轴负半轴的交点,且
轴负半轴的交点,且 ,求实数
,求实数 的取值范围.
的取值范围.
(本题满分12分)  某权威机构发布了2013年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城”.随后,该市某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某权威机构发布了2013年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城”.随后,该市某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记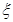 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求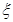 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)如图, 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 上除
上除 、
、 外的一个动点,
外的一个动点,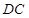 垂直于半圆
垂直于半圆 所在的平面,
所在的平面, 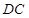 ∥
∥ ,
,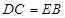 ,
, ,
,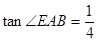 .
.
(1)证明:平面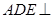 平面
平面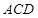 ;
;
(2)当三棱锥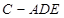 体积最大时,求二面角
体积最大时,求二面角 的余弦值.
的余弦值.
(本小题满分12分) 中内角
中内角 的对边分别为
的对边分别为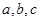 ,向量
,向量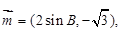
 且
且
(1)求锐角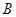 的大小;
的大小;
(2)如果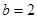 ,求
,求 的面积
的面积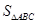 的最大值.
的最大值.
给出下列四个结论:
(1)如图 中,
中,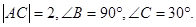 D是斜边AC上的点,|CD|=|CB|.以B为起点任作一条射线BE交AC于E点,则E点落在线段CD上的概率是
D是斜边AC上的点,|CD|=|CB|.以B为起点任作一条射线BE交AC于E点,则E点落在线段CD上的概率是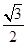 ;
;
(2)设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2, ,n),用最小二乘法建立的线性回归方程为 ,则若该大学某女生身高增加1 cm,则其体重约增加0.85 kg;
,则若该大学某女生身高增加1 cm,则其体重约增加0.85 kg;
(3)为调查中学生近视情况,测得某校男生150名中有80名近视,在140名女生中有70名近视.在检验这些学生眼睛近视是否与性别有关时,应该用独立性检验最有说服力;
(4)已知随机变量 服从正态分布
服从正态分布 则
则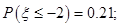
其中正确结论的个数为()
| A.1 | B.2 | C.3 | D.4 |