为了保护环境,某工厂在国家的号召下,把废弃物回收转化为某种产品,经测算,处理成本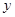 (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: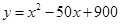 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴 万元.当
万元.当 时,判断该项举措能否获利?如果能获利,求出最大利润;如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
时,判断该项举措能否获利?如果能获利,求出最大利润;如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
已知定点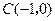 及椭圆
及椭圆 ,过点
,过点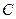 的动直线与椭圆相交于
的动直线与椭圆相交于 两点.
两点.
(Ⅰ)若线段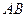 中点的横坐标是
中点的横坐标是 ,求直线
,求直线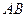 的方程;
的方程;
(Ⅱ)在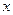 轴上是否存在点
轴上是否存在点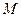 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点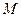 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
甲、乙两个射手进行射击训练,甲击中目标的概率为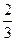 ,乙击中目标的概率为
,乙击中目标的概率为 ,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”.
,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”.
(1)求一个“单位射击组”为“单位进步组”的概率;(2)现要完成三个“单位射击组”,记出现“单位进步组”的次数为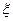 ,求
,求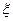 的分布列与数学期望.
的分布列与数学期望.
如图,在正四棱锥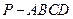 中,
中,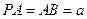 ,点
,点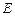 在棱
在棱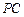 上. (Ⅰ)问点
上. (Ⅰ)问点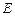 在何处时,
在何处时,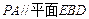 ,并加以证明;(Ⅱ)当
,并加以证明;(Ⅱ)当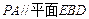 时,求点
时,求点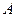 到平面
到平面 的距离;(Ⅲ)求二面角
的距离;(Ⅲ)求二面角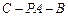 的大小.
的大小.
(本小题满分10分)已知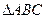 中,
中, ,
,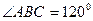 ,
,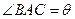 ,
, 记
记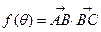 ,
,
(1)求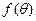 关于
关于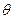 的表达式;
的表达式;
(2)求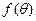 的值域;
的值域;
仔细阅读下面问题的解法:
设A=[0,1],若不等式21-x-a>0在A上有解,求实数a的取值范围。
解:由已知可得 a<21-x
令f(x)=21-x,∵不等式a<21-x在A上有解,
∴a<f(x)在A上的最大值.
又f(x)在[0,1]上单调递减,f(x)max ="f(0)=2." ∴实数a的取值范围为a<2.
研究学习以上问题的解法,请解决下面的问题:
(1)已知函数f(x)=x2+2x+3(-2≤x≤-1),求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)= ,x∈A,试判断g(x)的单调性(写明理由,不必证明);
,x∈A,试判断g(x)的单调性(写明理由,不必证明);
(3)若B={x| >2x+a–5},且对于(1)中的A,A∩B≠F,求实数a的取值范围。
>2x+a–5},且对于(1)中的A,A∩B≠F,求实数a的取值范围。