如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.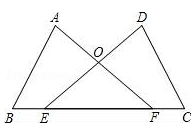
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.

根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生,其中安全意识为“很强”的学生占被调查学生总数的百分比是 ;
(2)请将条形统计图补充完整;
(3)该校有1800名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有 名.
如图,在四边形 中,
中, ,
, ,点
,点 在边
在边 上.
上.
(1)判断四边形 的形状并加以证明;
的形状并加以证明;
(2)若 ,以过点
,以过点 的直线为轴,将四边形
的直线为轴,将四边形 折叠,使点
折叠,使点 、
、 分别落在点
分别落在点 、
、 上,且
上,且 经过点
经过点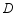 ,折痕与四边形的另一交点为
,折痕与四边形的另一交点为 .
.
①在图2中作出四边形 (保留作图痕迹,不必说明作法和理由);
(保留作图痕迹,不必说明作法和理由);
②如果 ,那么
为何值时,
,那么
为何值时, .
.

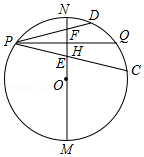
我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
如图,点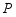 在以
在以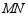 (南北方向)为直径的
(南北方向)为直径的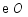 上,
上,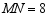 ,
,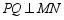 交
交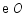 于点
于点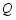 ,垂足为
,垂足为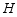 ,
,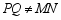 ,弦
,弦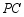 、
、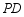 分别交
分别交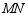 于点
于点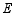 、
、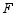 ,且
,且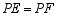 .
.
(1)比较 与 的大小;
(2)若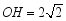 ,求证:
,求证: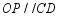 ;
;
(3)设直线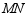 、
、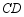 相交所成的锐角为
相交所成的锐角为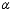 ,试确定
,试确定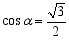 时,点
时,点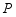 的位置.
的位置.
某进口专营店销售一种“特产”,其成本价是20元 千克,根据以往的销售情况描出销量
千克,根据以往的销售情况描出销量 (千克
(千克 天)与售价
天)与售价 (元
(元 千克)的关系,如图所示.
千克)的关系,如图所示.
(1)试求出 与
与 之间的一个函数关系式;
之间的一个函数关系式;
(2)利用(1)的结论:
①求每千克售价为多少元时,每天可以获得最大的销售利润.
②进口产品检验、运输等过程需耗时5天,该“特产”最长的保存期为一个月 天),若售价不低于30元
天),若售价不低于30元 千克,则一次进货最多只能多少千克?
千克,则一次进货最多只能多少千克?

已知反比例函数的图象经过点 .
.
(1)求该函数的解析式;
(2)若将点 沿
沿 轴负方向平移3个单位,再沿
轴负方向平移3个单位,再沿 轴方向平移
轴方向平移 个单位得到点
个单位得到点 ,使点
,使点 恰好在该函数的图象上,求
恰好在该函数的图象上,求 的值和点
的值和点 沿
沿 轴平移的方向.
轴平移的方向.