如图,在平面直角坐标系中,O是原点,已知A(4,3),P是y轴上的动点,当点O,A,P
三点组成的三角形为等腰三角形时,求出所有符合条件的点P坐标.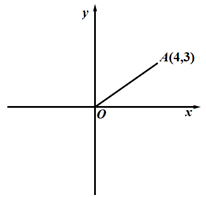
定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径. 如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段.
在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由. 友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由. 若此时AB=3,BD=
 ,求BC的长.
,求BC的长.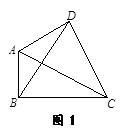


如图,抛物线 与
与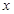 轴相交于
轴相交于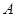 、
、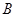 两点(点
两点(点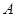 在点
在点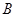 的左侧),与
的左侧),与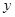 轴相交于点
轴相交于点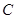 ,顶点为
,顶点为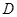 .
.
直接写出
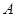 、
、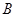 、
、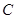 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;连接
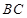 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点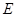 ,点
,点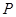 为线段
为线段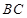 上的一个动点,过点
上的一个动点,过点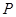 作
作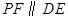 交抛物线于点
交抛物线于点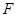 ,设点
,设点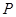 的横坐标为
的横坐标为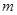 ;
;
①用含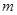 的代数式表示线段
的代数式表示线段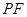 的长,并求出当
的长,并求出当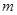 为何值时,四边形
为何值时,四边形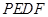 为平行四边形?
为平行四边形?
②设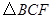 的面积为
的面积为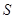 ,求
,求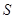 与
与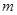 的函数关系式.
的函数关系式.
据悉,某市发改委拟于今年4月27日举行居民用水价格调整听证会,届时将有两个方案提供听证。如图(1),射线OA、射线OB分别表示现行的、方案一的每户每月的用水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;方案二如图(2)表格所示,每月的每立方米用水价格由该月的用水量决定,且第一、二、三级的用水价格之比为1︰1.5︰2(精确到0.01元后).写出现行的用水价是每立方米多少元?
求图(1)中m的值和射线OB所对应的函数解析式,并写出定义域;
若小明家某月的用水量是a立方米,请分别写出三种情况下(现行的、方案一和方案二)该月的水费b(用a的代数式表示);
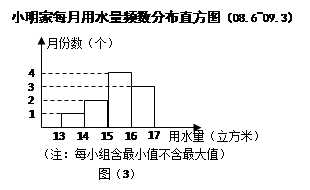
小明家最近10个月来的每月用水量的频数分布直方图
如图(3)所示,估计小明会赞同采用哪个方案?请说明理由。 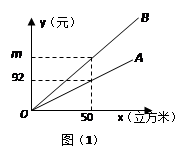
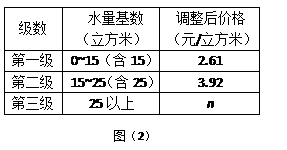
如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60º.求⊙O的直径;
若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
若动点E以2cm/s的速度从A点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动,设运动时间为
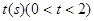 ,连结EF,当
,连结EF,当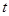 为何值时,△BEF为直角三角形.
为何值时,△BEF为直角三角形.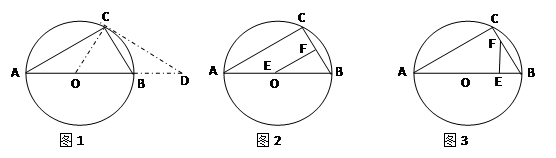
有两个可以自由转动的均匀转盘 ,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘 ;
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).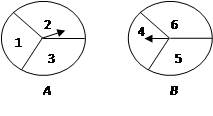
用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.