如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60º.
求⊙O的直径;
若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
若动点E以2cm/s的速度从A点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动,设运动时间为
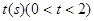 ,连结EF,当
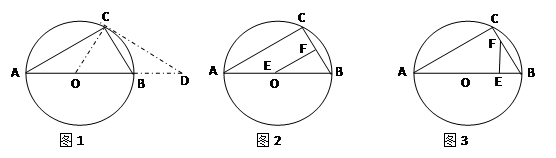
,连结EF,当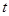 为何值时,△BEF为直角三角形.
为何值时,△BEF为直角三角形.
抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).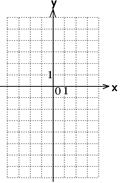
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点坐标;
(3)画出这条抛物线大致图象;
(4)根据图象回答:
①当x取什么值时,y>0 ?
②当x取什么值时,y的值随x的增大而减小?
如图,已知反比例函数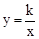 与一次函数
与一次函数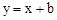 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1,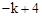 ),
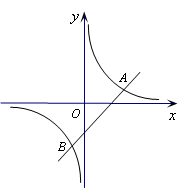
),
(1)试确定这两个函数的表达式;
(2)求出这两个函数图像的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D.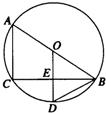
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径.
已知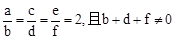 .
.
(1)求 的值;(2)若
的值;(2)若 ,求
,求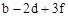 的值.
的值.
如图,已知△ABC中,BD、CE是高,F是BC中点,连接DE、EF和DF.
(1)求证:△DEF是等腰三角形;
(2)若∠A=45°,试判断△DEF的形状,并说明理由;
(3)若∠A:∠DFE=5:2,BC=4,求△DEF的面积.