无锡市中考体育考试方案公布后,同学们将根据自己平时的运动成绩确定自己的报考项目,下面是小亮同学在近期的两个项目中连续五次测试的得分情况(立定跳远得分统计表和一分钟跳绳的折线图):

| 统计量 |
平均数 |
极差 |
方差 |
| 立定跳远 |
8 |
|
|
| 一分钟跳绳 |
|
2 |
0.4 |
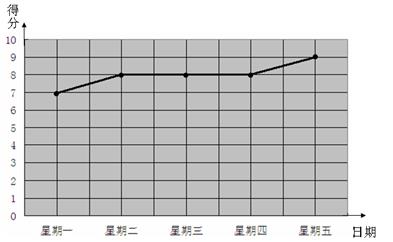
(1)请把立定跳远的成绩通过描点并且用虚线在折线图中画出来.
(2)请根据以上信息,分别将这两个项目的平均数、极差、方差填入下表:
(3)根据以上信息,你认为在立定跳远和一分钟跳绳这两个项目中,小亮应选择哪个项目作为体育考试的报考项目?请简述理由.
已知两直线l1,l2分别经过点A(1,0),点B(-3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.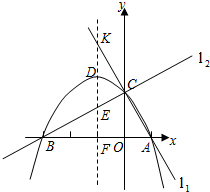
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1、抛物线、直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标:
有一种产品的质量分成6种不同档次,若工时不变,每天可生产最低档次的产品40件;如果每提高一个档次,每件利润可增加1元,但每天要少生产2件产品。
⑴若最低档次的产品每件利润17元时,生产哪一种档次的产品的利润最大?并求最大利润。
⑵由于市场价格浮动,生产最低档次的产品每件利润可以从8元到24元不等,那么生产哪种档次的产品所得利润最大?
阅读下面的情境对话,然后解答问题
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
1求证: ACE是奇异三角形;
ACE是奇异三角形;
2当 ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
自变量为x的二次函数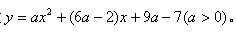
(1)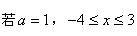 ,求函数值y的最大值与最小值;并分别指出所对应的自变量x的值;
,求函数值y的最大值与最小值;并分别指出所对应的自变量x的值;
(2)当a变化时,该二次函数图象是否经过定点?若是,请求出定点坐标;若不是,请说明理由;
(3)若该二次函数图象与x轴有两个不同的交点,而且两交点的横坐标均小于-1,求a的取值范围。
如图1,有一张菱形纸片ABCD,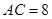 ,
, .
.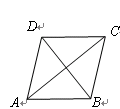
(1)请沿着AC剪一刀,把它分成两部分,把剪开的两部分拼成一个平行四边形,在图2中用实数画出你所拼成的平行四边形;若沿着BD剪开,请在图3中用实线画出拼成的平行四边形;并直接写出这两个平行四边形的周长.
(2)沿着一条直线剪开,拼成与上述两种都不全等的平行四边形,请在图4中用实线画出拼成的平行四边形.
(注:上述所画的平行四边形都不能与原菱形全等)
周长为__________周长为__________