如图，Rt△ABC的三个顶点分别是A（－3，2），B（0，4-优题课

某汽车销售公司一位销售经理 $1 ~ 5$ 月份的汽车销售统计图如下：

（1）已知1月的销售量是2月的销售量的3.5倍，则1月的销售量为　　辆．在图2中，2月的销售量所对应的扇形的圆心角大小为　　．

（2）补全图1中销售量折线统计图．

（3）已知4月份销售的车中有3辆国产车和2辆合资车，国产车分别用 $G_{1}$ 、 $G_{2}$ 、 $G_{3}$ 表示，合资车分别用 $H_{1}$ 、 $H_{2}$ 表示，现从这5辆车中随机抽取两辆车参加公司的回馈活动，请用列举法（画树状图或列表）求出“抽到的两辆车都是国产车“的概率．

如图，在四边形 $ABCD$ 中， $BC / / AD$ ， $BC = \frac{1}{2} AD$ ，点 $E$ 为 $AD$ 的中点，点 $F$ 为 $AE$ 的中点， $AC ⊥ CD$ ，连接 $BE$ 、 $CE$ 、 $CF$ ．

（1）判断四边形 $ABCE$ 的形状，并说明理由；

（2）如果 $AB = 4$ ， $∠ D = 30 °$ ，点 $P$ 为 $BE$ 上的动点，求 $ΔPAF$ 的周长的最小值．

计算： $- 1^{2} + {(2 - \sqrt{2})}^{0} - 4 \cos 60 ° - \sqrt[3]{- 8}$ ．

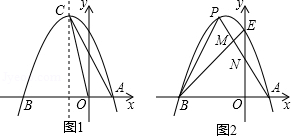
如图1，已知抛物线 $y = - x^{2} + bx + c$ 过点 $A (1, 0)$ ， $B (- 3, 0)$ ．

（1）求抛物线的解析式及其顶点 $C$ 的坐标；

（2）设点 $D$ 是 $x$ 轴上一点，当 $\tan (∠ CAO + ∠ CDO) = 4$ 时，求点 $D$ 的坐标；

（3）如图2．抛物线与 $y$ 轴交于点 $E$ ，点 $P$ 是该抛物线上位于第二象限的点，线段 $PA$ 交 $BE$ 于点 $M$ ，交 $y$ 轴于点 $N$ ， $ΔBMP$ 和 $ΔEMN$ 的面积分别为 $m$ 、 $n$ ，求 $m - n$ 的最大值．

箭头四角形

模型规律

如图1，延长 $CO$ 交 $AB$ 于点 $D$ ，则 $∠ BOC = ∠ 1 + ∠ B = ∠ A + ∠ C + ∠ B$ ．

因为凹四边形 $ABOC$ 形似箭头，其四角具有“ $∠ BOC = ∠ A + ∠ B + ∠ C$ ”这个规律，所以我们把这个模型叫做“箭头四角形”．

模型应用

（1）直接应用：①如图2， $∠ A + ∠ B + ∠ C + ∠ D + ∠ E + ∠ F =$ 　 $2 α$ 　．

②如图3， $∠ ABE$ 、 $∠ ACE$ 的2等分线（即角平分线） $BF$ 、 $CF$ 交于点 $F$ ，已知 $∠ BEC = 120 °$ ， $∠ BAC = 50 °$ ，则 $∠ BFC =$ 　　．

③如图4， $B O_{i}$ 、 $C O_{i}$ 分别为 $∠ ABO$ 、 $∠ ACO$ 的2019等分线 $(i = 1$ ，2，3， $\dots$ ，2017， $2018)$ ．它们的交点从上到下依次为 $O_{1}$ 、 $O_{2}$ 、 $O_{3}$ 、 $\dots$ 、 $O_{2018}$ ．已知 $∠ BOC = m °$ ， $∠ BAC = n °$ ，则 $∠ B O_{1000} C =$ 　　度．

（2）拓展应用：如图5，在四边形 $ABCD$ 中， $BC = CD$ ， $∠ BCD = 2 ∠ BAD$ ． $O$ 是四边形 $ABCD$ 内一点，且 $OA = OB = OD$ ．求证：四边形 $OBCD$ 是菱形．