阅读下列材料并解决有关问题:
我们知道,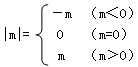 现在我们可以用这一结论来化简含有绝对值
现在我们可以用这一结论来化简含有绝对值
的代数式,如化简代数式|m+1|+|m-2|时,可令m+1=0和m-2=0,分别求得m=-1,m=2(称-1,2分别为|m+1|与|m-2|的零点值).在实数范围内,零点值m=-1和m=2可将全体实数分成不重复且不遗漏的如下3种情况:
(1)m<-1;(2)-1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m-2|可分以下3种情况:
(1)当m<-1时,原式=-(m+1)-(m-2)=-2m+1;
(2)当-1≤m<2时,原式=m+1-(m-2)=3;
(3)当m≥2时,原式=m+1+m-2=2m-1.
综上讨论,原式=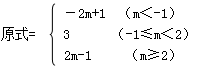
通过以上阅读,请你解决以下问题:
(1)分别求出|x-5|和|x-4|的零点值;
(2)化简代数式|x-5|+|x-4|.
(3)求代数式|x-5|+|x-4|的最小值.
如图,矩形ABCD中,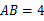 cm,
cm,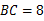 cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且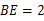 cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,请猜想,CE和CF的大小有什么关系?并证明你的猜想.
商场销售某种产品,一月份销售了若干件,共获利润30 000元.二月份将这种商品的单价降低了0.4元.但销售量比一月份增加了5 000件,从而获得利润比一月份多2 000元. 求调价前每件商品的利润是多少元?
如图,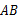 是⊙
是⊙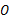 的直径,
的直径,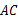 是⊙
是⊙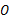 的弦,以
的弦,以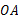 为直径的⊙
为直径的⊙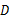 与
与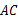 相交于点
相交于点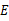 ,
,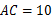 ,求
,求 的长.
的长.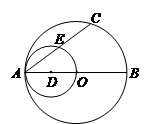
如图, 、
、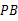 是⊙O的两条切线,
是⊙O的两条切线,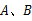 是切点,
是切点, 是⊙
是⊙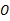 的直径,若∠
的直径,若∠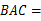 40°,求∠
40°,求∠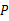 的度数.
的度数.