如图,直线y=kx+b与y轴交于点A,与x轴交于点B,边长为2的等边ΔCOD的顶点C、D分别在线段AB、OB上,且DO=2DB.

(1)求B、C两点的坐标;
(2)求直线AB的解析式.
△OAB的坐标分别为O(0, 0),A(0,4),B(3,0),以原点为位似中心,在第一象限将△OAB扩大,使变换得到的△OEF与△OAB对应边的比为2:1 ,
(1)画出△OEF;
(2)求四边形ABFE的面积.
如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=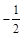 x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=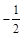 x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.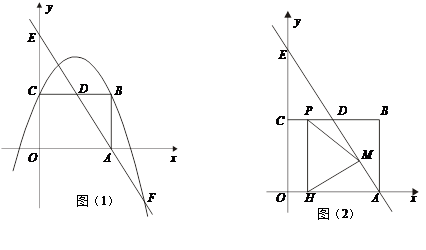
(1)求该抛物线解析式与F点坐标;
(2)如图,动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;
同时,动点M从点A出发,沿线段AE以每秒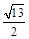 个单位长度的速度向终点E运动.过
个单位长度的速度向终点E运动.过
点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
①问EP+PH+HF是否有最小值,如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,求出此时t的值.
探究:如图(1),在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=900,连接AC,EF。在图中找一个与△FAE全等的三角形,并加以证明。
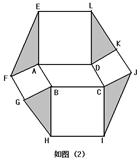
应用:以□ABCD的四条边为边,在其形外分别作正方形,如图(2),连接EF,GH,IJ,KL。若□ABCD的面积为6,则图中阴影部分四个三角形的面积和为____________.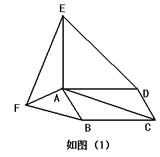
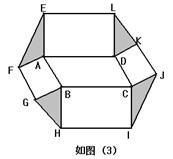
推广:以□ABCD的四条边为矩形长边,在其形外分别作长与宽之比为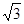 矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12
矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12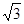 ,求□ABCD的面积?
,求□ABCD的面积?
如图,已知A,B两点的坐标分别为A(0,2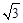 ),B(2,0)直线AB与反比例函数
),B(2,0)直线AB与反比例函数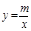 的图像交与点C和点D(-1,
的图像交与点C和点D(-1,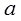 ).
).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数;
(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.
已知:图1为一锐角是30°的直角三角尺,其边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).
操作:将三角尺移向直径为4cm的⊙O,它的内Rt△ABC的斜边AB恰好等于⊙O的直径,它的外Rt△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2)。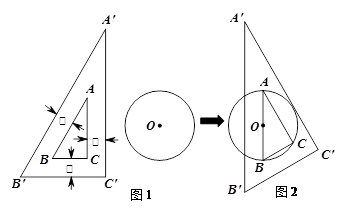
思考:(1) 求直角三角尺边框的宽。
(2) 求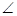 BB′C′+
BB′C′+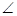 CC′B′的度数。
CC′B′的度数。
(3) 求边B′C′的长。