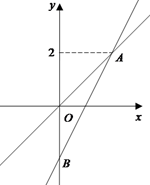《中国足球改革总体方案》提出足球要进校园．为了解某校学生对校园足球喜爱的情况，随机对该校部分学生进行了调查，将调查结果分为“很喜欢”、“较喜欢”、“一般”、“不喜欢”四个等级，并根据调查结果绘制成了如下两幅不完整的统计图：
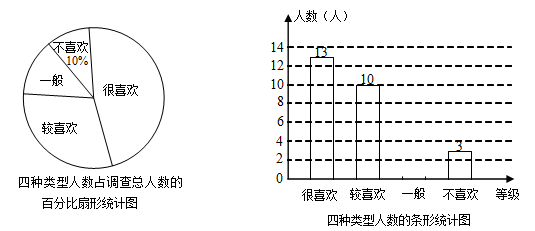
（1）一共调查了 名学生，请补全条形统计图；
（2）在此次调查活动中，选择“一般”的学生中只有两人来自初三年级．现在要从选择“一般”的同学中随机抽选两人来谈谈各自对校园足球的感想，请用画树状图或列表法求选中的两人刚好都来自初三年级的概率．
如图1，在平面直角坐标系xOy中，等腰直角△AOB的斜边OB在x上，顶点A的坐标为（3，3）.
（1）求直线OA的解析式；
（2）如图2，如果点P是x轴正半轴上的一个动点，过点P作PC∥y轴，交直线OA于点C，设点P的坐标为（m，0），以A、C、P、B为顶点的四边形面积为S，求S与m之间的函数关系式；
（3）如图3，如果点D（2，a）在直线AB上. 过点O、D作直线OD，交直线PC于点E，在CE的右侧作矩形CGFE，其中CG=
，请你直接写出矩形CGFE与△AOB重叠部分为轴对称图形时m的取值范围.
图1图2图3
阅读下列材料：
问题：如图1，在□ABCD中，E是AD上一点，AE=AB，∠EAB=60°，过点E作直线
EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG.
求证：EG =AG+BG.
小明同学的思路是：作∠GAH=∠EAB交GE于点H，构造全等三角形，经过推理使
问题得到解决.
参考小明同学的思路，探究并解决下列问题：
（1）完成上面问题中的证明；
（2）如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”，原问题中的其它条件不变（如图2），请探究线段EG、AG、BG之间的数量关系，并证明你的结论.
图1图2
已知：关于x的方程mx2+(3m+1)x+3=0．
（1）求证：不论m为任何实数，此方程总有实数根；
（2）如果该方程有两个不同的整数根，且m为正整数，求m的值；
（3）在（2）的条件下，令y=mx2+(3m+1)x+3，如果当x1=a与x2=a+n（n≠0）时有y1=y2，求代数式4a2+12an+5n2+16n+8的值．
列方程（组）解应用题：
据媒体报道，2011年某市市民到郊区旅游总人数约500万人，2013年到郊区旅游总
人数增长到约720万人．
（1）求这两年该市市民到郊区旅游总人数的年平均增长率．
（2）若该市到郊区旅游的总人数年平均增长率不变，请你预计2014年有多少市民到郊区旅游．
如图，在平面直角坐标系xOy中，正比例函数y=x的图象与一次函数y=kx－k的图象的交点坐标为A（m，2）．
（1）求m的值和一次函数的解析式；
（2）设一次函数y=kx－k的图象与y轴交于点B，求△AOB的面积；
（3）直接写出使函数y=kx－k的值大于函数y=x的值的自变量x的取值范围．