已知椭圆C的中心O为坐标原点,右焦点为F(1,0),A、B分别是椭圆C的左右顶点,P是椭圆C上的动点.
(Ⅰ)若△PAB面积的最大值为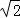 ,求椭圆C的方程;
,求椭圆C的方程;
(Ⅱ)过右焦点F做长轴AB的垂线,交椭圆C于M、N两点,若|MN|=3,求椭圆C的离心率.
已知等差数列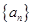 满足:
满足: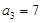 ,
, .
.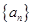 的前
的前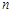 项和为
项和为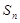 .
.
(1)求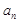 及
及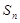 ;
;
(2)令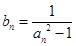
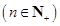 ,求数列
,求数列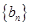 的前
的前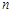 项和
项和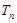 .
.
(1)若不等式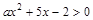 的解集是
的解集是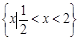 ,求不等式
,求不等式 的解集.
的解集.
(2)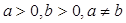 ,试比较
,试比较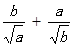 与
与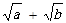 的大小。
的大小。
设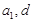 为实数,首项为
为实数,首项为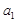 ,公差为
,公差为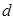 的等差数列
的等差数列 的前
的前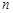 项和为
项和为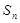 ,满足
,满足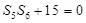 .
.
(1)若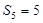 求
求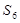 及
及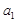 ;
;
(2)求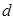 的取值范围.
的取值范围.
椭圆C: 的离心率为
的离心率为 ,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2),设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T.求证:点T在椭圆C上.
设数列 的前项n和为
的前项n和为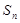 ,若对于任意的正整数n都有
,若对于任意的正整数n都有 .
.
(1)设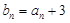 ,求证:数列
,求证:数列 是等比数列,并求出
是等比数列,并求出 的通项公式。
的通项公式。
(2)求数列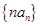 的前n项和.
的前n项和.