对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知函数f(x)=ax2+(b+1)x+b﹣1(a≠0).
(1)当a=1,b=﹣2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
(本小题满分12分)
已知数列{a }的前n项和Sn= —a
}的前n项和Sn= —a —(
—(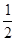 )
) +2 (n为正整数).
+2 (n为正整数).
(1)证明:a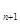 =
=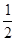 a
a + (
+ (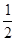 )
) .,并求数列{a
.,并求数列{a }的通项
}的通项
(2)若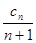 =
= ,T
,T = c
= c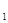 +c
+c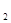 +···+c
+···+c ,求T
,求T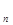 .
.
(本小题满分12分)
已知函数 .
.
(1)求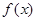 的单调递增区间;
的单调递增区间;
(2)在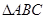 中,角
中,角 ,
,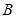 ,
,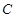 的对边分别为
的对边分别为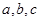 .已知
.已知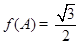 ,
, ,试判断
,试判断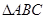 的形状.
的形状.
(本小题满分14分)已知函数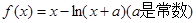 .
.
(1)求函数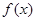 的单调区间;
的单调区间;
(2)当 处取得极值时,若关于
处取得极值时,若关于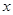 的方程
的方程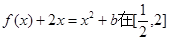 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)求证:当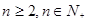 时,有
时,有
(本小题满分13分)
动圆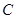 与定圆
与定圆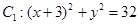 内切,与定圆
内切,与定圆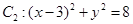 外切,A点坐标为
外切,A点坐标为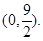
(1)求动圆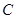 的圆心
的圆心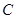 的轨迹方程和离心率;
的轨迹方程和离心率;
(2)若轨迹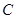 上的两点
上的两点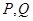 满足
满足 ,求
,求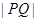 的值.
的值.
(本小题满分12分)如图,在三棱锥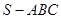 中,底面
中,底面 是边长为4的正三角形,平面
是边长为4的正三角形,平面
 ,M,N分别为AB,SB的中点.
,M,N分别为AB,SB的中点.
(1)求证: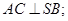
(2)求二面角 的余弦值.
的余弦值.