(本小题满分13分)
动圆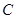 与定圆
与定圆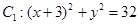 内切,与定圆
内切,与定圆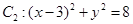 外切,A点坐标为
外切,A点坐标为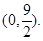
(1)求动圆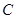 的圆心
的圆心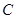 的轨迹方程和离心率;
的轨迹方程和离心率;
(2)若轨迹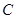 上的两点
上的两点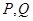 满足
满足 ,求
,求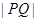 的值.
的值.
如图,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
(1)若=,求证:无论点P在D1D上如何移动,总有BP⊥MN;
(2)若D1P:PD=1∶2,且PB⊥平面B1MN,求二面角M-B1N-B的余弦值;
(3)棱DD1上是否总存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.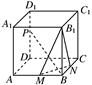
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;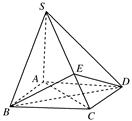
如图所示,四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠D=∠DAB=90°,AB=4,CD=1,AD=2.
(1)建立适当的坐标系,并写出点B,P的坐标;
(2)求异面直线PA与BC所成角的余弦值;
(3)若PB的中点为M,求证:平面AMC⊥平面PBC.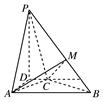
如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.
(1)证明:平面PAB⊥平面PCM;
(2)证明:线段PC的中点为球O的球心
在矩形ABCD中,AB=1,BC=a,现沿AC折成二面角D-AC-B,使BD为异面直线AD、BC的公垂线.
(1)求证:平面ABD⊥平面ABC;
(2)当a为何值时,二面角D-AC-B为45°