二次函数f（x）的图象顶点为A（1，16），且图象在x轴上截得线段长为8．
（1）求函数f（x）的解析式；
（2）令g（x）=（2﹣2a）x﹣f（x）；
①若函数g（x）在x∈[0，2]上是单调增函数，求实数a的取值范围；
②求函数g（x）在x∈[0，2]的最小值．
已知函数
是奇函数．
（1）求实数m的值；
（2）是否存在实数
，当
时，函数
的值域是
．若存在，求出实数；若不存在，说明理由；
（3）令函数
，当
时，求函数
的最大值．
如图，在长为10千米的河流OC的一侧有一条观光带，观光带的前一部分为曲线段OAB，设曲线段OAB为函数
，
（单位：千米）的图象，且图象的最高点为
；观光带的后一部分为线段BC．
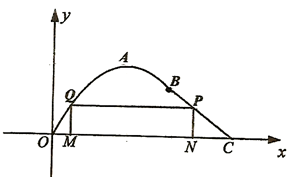
（1）求函数为曲线段OABC的函数
的解析式；
（2）若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ，绿化带由线段MQ，QP，PN构成，其中点P在线段BC上．当OM长为多少时，绿化带的总长度最长？
已知函数f（x）＝2ax＋
（a∈R）．
（1）当
时，试判断f（x）在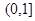
上的单调性并用定义证明你的结论；
（2）对于任意的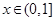
，使得f（x）≥6恒成立，求实数a的取值范围．
已知函数
为幂函数，且为奇函数．
（1）求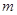
的值；
（2）求函数
在
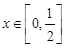的值域．
设
，a为实数．
（1）分别求
；
（2）若
，求a的取值范围．