已知函数f(x)=ax2+bx+1(a,b∈R且a≠0),F(x)=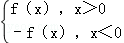 .
.
(1)若f(﹣1)=0,且函数f(x)的值域为[0,+∞),求F(x)的解析式;
(2)在(1)的条件下,当x∈[﹣2,2]时,g(x)=f(x)﹣kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)是偶函数,判断F(m)+F(n)是否大于零.
(本小题共13分)
已知椭圆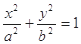
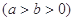 和直线L:
和直线L: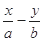 ="1," 椭圆的离心率
="1," 椭圆的离心率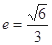 ,直线L与坐标原点的距离为
,直线L与坐标原点的距离为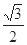 。
。
(1)求椭圆的方程;
(2)已知定点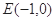 ,若直线
,若直线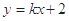
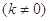 与椭圆相交于C、D两点,试判断是否存在
与椭圆相交于C、D两点,试判断是否存在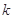 值,使以CD为直径的圆过定点E?若存在求出这个
值,使以CD为直径的圆过定点E?若存在求出这个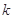 值,若不存在说明理由。
值,若不存在说明理由。
(本小题共14分)
已知函数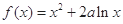 .
.
(Ⅰ)若函数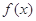 的图象在
的图象在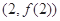 处的切线斜率为
处的切线斜率为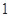 ,求实数
,求实数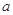 的值;
的值;
(Ⅱ)求函数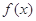 的单调区间;
的单调区间;
(Ⅲ)若函数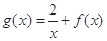 在
在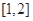 上是减函数,求实数
上是减函数,求实数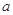 的取值范围.
的取值范围.
(本小题共14分)
如图所示多面体中,AD⊥平面PDC,ABCD为平行四边形,E,F分别为AD,BP的中点,AD=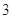 ,AP=
,AP=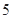 ,PC=
,PC=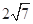 .
.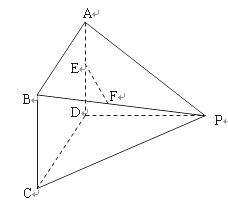
(Ⅰ)求证:EF∥平面PDC;
(Ⅱ)若∠CDP=90°,求证BE⊥DP;
(Ⅲ)若∠CDP=120°,求该多面体的体积.
(本小题共13分)
已知等差数列 的前
的前 项和为
项和为 ,且
,且
(1)求 通项公式;
通项公式;
(2)求数列 的前
的前 项和
项和
(本小题共13分)
某小区在一次对20岁以上居民节能意识的问卷调查中,随机抽取了100份问卷进行统计,得到相关的数据如下表:
(1)由表中数据直观分析,节能意识强弱是否与人的年龄有关?
(2)据了解到,全小区节能意识强的人共有350人,估计这350人中,年龄大于50岁的有多少人?
(3)按年龄分层抽样,从节能意识强的居民中抽5人,再从这5人中任取2人,求恰有1人年龄在20至50岁的概率。