已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=2,任取a,b∈[﹣1,1],a+b≠0,都有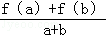 >0成立.
>0成立.
(1)证明函数f(x)在[﹣1,1]上是单调增函数.
(2)解不等式f(x)<f(x2).
(3)若对任意x∈[﹣1,1],函数f(x)≤2m2﹣2am+3对所有的a∈[0, ]恒成立,求m的取值范围.
]恒成立,求m的取值范围.
(本小题满分14分)
设
(1)若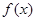 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数 的取值范围;
的取值范围;
(2)设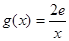 ,且
,且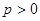 ,若在
,若在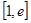 上至少存在一点
上至少存在一点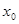 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明: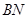 ⊥平面
⊥平面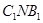 ;
;
(Ⅱ)求平面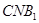 与平面
与平面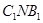 所成角的余弦值;
所成角的余弦值;
(本小题12分)为了丰富学生的课余生活,促进校园文化建设,我校高二年级通过预赛选出了6个班(含甲、乙)进行经典美文颂读比赛决赛.决赛通过随机抽签方式决定出场顺序.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)决赛中甲、乙两班之间的班级数记为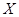 ,求
,求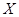 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
在极坐标系中,已知圆C的圆心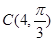 ,半径r=2,Q点在圆C上运动。
,半径r=2,Q点在圆C上运动。
(I)求圆C的极坐标方程;
(II)若P在直线OQ上运动,且OQ∶OP=3∶2,求动点P的轨迹方程。
(本小题满分12分)已知点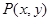 是圆
是圆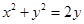 上的动点,
上的动点,
(1)求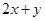 的取值范围;
的取值范围;
(2)若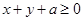 恒成立,求实数
恒成立,求实数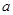 的取值范围。
的取值范围。