已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0,
(1)求证:直线l恒过定点;
(2)判断直线l被圆C截得的弦长何时最长,何时最短?并求截得的弦长最短时,求m的值以及最短长度.
已知 的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的
的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的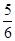
(Ⅰ)求展开后所有项的系数之和及所有项的二项式系数之和;
(Ⅱ)求展开式中的有理项.
(1)在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值.
(2)对5副不同的手套进行不放回抽取,甲先任取一只,乙再任取一只,然后甲又任取一只,最后乙再任取一只.对于下列事件:①A:甲正好取得两只配对手套;②B:乙正好取得两只配对手套.试判断事件A与B是否独立?并证明你的结论.
已知△ABC中,A(2,4),B(-1,-2),C(4,3),BC边上的高为AD.
⑴求证:AB⊥AC;
⑵求点D与向量 的坐标.
的坐标.
已知函数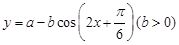 的最大值为
的最大值为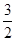 ,最小值为
,最小值为 .
.
(1)求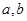 的值;
的值;
(2)求函数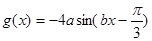 的最小值并求出对应x的集合.
的最小值并求出对应x的集合.
已知: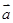 、
、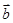 、
、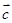
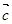 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中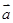 =(1,2)
=(1,2)
(1)若| 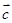 |
|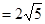 ,且
,且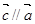 ,求
,求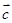 的坐标;
的坐标;
(2)若| 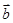 |=
|=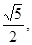 且
且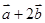 与
与 垂直,求
垂直,求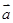 与
与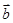 的夹角
的夹角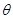 .
.