如图,直三棱柱ABC﹣A′B′C′,∠BAC=90°, ,AA′=1,点M,N分别为A′B和B′C′的中点.
,AA′=1,点M,N分别为A′B和B′C′的中点.
(Ⅰ)证明:MN∥平面A′ACC′;
(Ⅱ)求三棱锥A′﹣MNC的体积.
(椎体体积公式V= Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)
(本小题满分13分)设数列 的前
的前 项和为
项和为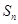 ,点
,点 均在函数
均在函数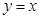 的图象上.
的图象上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 为等比数列,且
为等比数列,且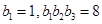 ,求数列
,求数列 的前n项和
的前n项和 .
.
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且AM ,点P是平面ABCD上的动点,且动点P到直线A1D1的距离与点P到点M的距离的平方差为1,则动点P的轨迹是()
,点P是平面ABCD上的动点,且动点P到直线A1D1的距离与点P到点M的距离的平方差为1,则动点P的轨迹是()
| A.圆 | B.抛物线 | C.双曲线 | D.椭圆 |
(本小题满分13分)设数列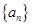 满足:
满足:
① ;
;
②所有项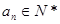 ;
;
③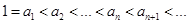 .
.
设集合 ,将集合
,将集合 中的元素的最大值记为
中的元素的最大值记为 ,即
,即 是数列
是数列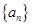 中满足不等式
中满足不等式 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列 为数
为数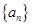 的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(Ⅰ)若数列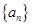 的伴随数列为1,1,1,2,2,2,3,请写出数列
的伴随数列为1,1,1,2,2,2,3,请写出数列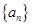 ;
;
(Ⅱ)设 ,求数列
,求数列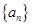 的伴随数列
的伴随数列 的前30项之和;
的前30项之和;
(Ⅲ)若数列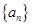 的前
的前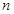 项和
项和 (其中
(其中 常数),求数列
常数),求数列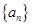 的伴随数列
的伴随数列
的前 项和
项和 .
.
(本小题满分14分)已知椭圆C: 离心率
离心率 ,短轴长为
,短轴长为 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ) 如图,椭圆左顶点为A,过原点O的直线(与坐标轴不重合)与椭圆C交于P,Q两点,直线PA,QA分别与y轴交于M,N两点.试问以MN为直径的圆是否经过定点(与直线PQ的斜率无关)?请证明你的结论.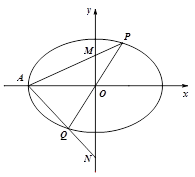
(本小题满分13分)已知函数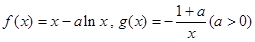 .
.
(Ⅰ)若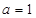 ,求函数
,求函数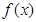 的极值;
的极值;
(Ⅱ)设函数 ,求函数
,求函数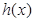 的单调区间;
的单调区间;
(Ⅲ)若存在 ,使得
,使得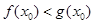 成立,求
成立,求 的取值范围.
的取值范围.